


Next: EEL6825: HW#5
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#3
Get PDF file
Due Friday, October 19, 2001 in class. Late homework will
lose
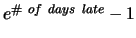 percentage points. Click on
http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
to see the current penalty.
As before, your homework should be in two distinct sections. The
first section should show the answers, explanations, plots, hand
calculations etc. that you need to answer the questions in parts
A-B. The second section should contain all of the Matlab code
that you have written to generate the answers in the first
section. You don't need a computer for most of part A but of
course you may use one to check your work if you like.
PART A: Textbook Problems Answer the following questions,
you should not need a computer.
percentage points. Click on
http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
to see the current penalty.
As before, your homework should be in two distinct sections. The
first section should show the answers, explanations, plots, hand
calculations etc. that you need to answer the questions in parts
A-B. The second section should contain all of the Matlab code
that you have written to generate the answers in the first
section. You don't need a computer for most of part A but of
course you may use one to check your work if you like.
PART A: Textbook Problems Answer the following questions,
you should not need a computer.
- A1
- You are given two two-dimensional data points. One occurs
at
![$[0,0]^T$](img40.gif) and the other at
and the other at ![$[1,1]^T$](img41.gif) .
.
- Derive the formula and sketch the Parzen windows estimate
of the pdf for a hypercube volume of
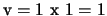 .
.
- Derive the formula and sketch the Parzen windows estimate
of the pdf for a hypercube volume of
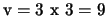 .
.
- Derive the formula and sketch the k-NN estimate
of the pdf for
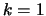 .
.
- Derive the formula and sketch the k-NN estimate
of the pdf for
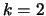 .
.
- A2
- Assuming that
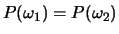 and that you are given
and that you are given 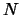 data points from each of two classes in
data points from each of two classes in 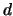 -dimensional space. The
Parzen classifier is expressed by
-dimensional space. The
Parzen classifier is expressed by
where the superscripts denote the class of each data point. Prove
that the leave-one-out error is larger than or equal to the
resubstitution error. Assume that
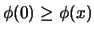 .
.
- A3
- You are given the following two 2-D distributions:
Assume that
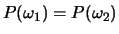 and a large number of
samples is available. Answer the following questions:
and a large number of
samples is available. Answer the following questions:
- Compute the expected probability of error for the ideal
Bayes classifier.
- Compute the expected probability of error for the 1-NN leave-one-out
procedure.
- Compute the expected probability of error for the 2-NN leave-one-out
procedure. Do not include the sample being classified and assume that
ties are rejected.
- Explain why the 2-NN error computed in part (c) is less than the Bayes
error.
- A4
- Consider the following sample points: The samples from class 1
are:
![$ \left[\begin{array}{c} 0 0 \end{array} \right]
\left[\begin{array}{c} 1 1 \end{array} \right]
\left[\begin{array}{c} 2 1 \end{array} \right] $](img51.gif) The samples from class 2 are:
The samples from class 2 are:
![$ \left[ \begin{array}{c} 1 0
\end{array} \right] \left[ \begin{array}{c} 1 ...
... -1 \end{array} \right] \left[
\begin{array}{c} 1 -2 \end{array} \right]$](img52.gif) Sketch the 1-NN
class boundaries for the this set of sample points.
Sketch the 1-NN
class boundaries for the this set of sample points.
- A5
- For the same points as in A4, sketch the 2-NN class boundaries for
the above set of sample points. Make sure you indicate the reject region.
PART B: Computer Experiment: Mines/rocks with nearest
neighbor classifier
Use the mines and rocks dataset from HW#4 to complete the
following problems:
- B1
- Design a nearest-neighbor classifier that chooses the class of the
nearest-neighbor for each point. What are the resubstitution and the
leave-one-out errors? How do these values compare to the linear classifier error from Homework #3?
Clearly indicate these results in your answers.
Programming hint: Do not use all of the data points when you are
developing your code. When you are confident that your program is
correct, run with the full number of points. Also, write your code with
efficiency in mind. If the full number of points still takes too long to
run, use as many points as you think reasonable but explain what you have
done.
- B2
- How long does it take for your program to classify all
of the data points? Answer this question by providing both the actual time
(e.g. using something like cputime in matlab)
and the number of floating point operations performed (e.g. using
something like the flops command in matlab). Also provide the
speed and model of your computer.
- B3
- Plot a graph that shows the leave-one-out performance of your
classifier that on a
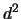 display like we discussed in class. The Y-axis
represents the distance between each point in the data set and its nearest
neighbor in the mines class. If the data point happens to come from the
mines class, leave it out of the minimum distance computation. Similarly,
the X-axis is the distance between each data point and its nearest
neighbor in the rocks class. (None of the distances should be exactly
zero since you are using the leave-one-out method and no points are
exactly repeated.)
display like we discussed in class. The Y-axis
represents the distance between each point in the data set and its nearest
neighbor in the mines class. If the data point happens to come from the
mines class, leave it out of the minimum distance computation. Similarly,
the X-axis is the distance between each data point and its nearest
neighbor in the rocks class. (None of the distances should be exactly
zero since you are using the leave-one-out method and no points are
exactly repeated.)
- B4
- Plot a line on the plot from [B3] that shows your solution to
problem [B1].
- B5
- Plot a second line in the
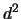 plot that
achieves the lowest error you can. What is the error? Since the
plot that
achieves the lowest error you can. What is the error? Since the
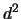 plot leaves out the distances to the same points, is this
error still the leave-one-out error? Or is it the resubstitution
error for the classifier? Explain.
plot leaves out the distances to the same points, is this
error still the leave-one-out error? Or is it the resubstitution
error for the classifier? Explain.



Next: EEL6825: HW#5
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#3
Dr John Harris
2001-11-26
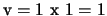 .
.
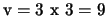 .
.
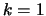 .
.
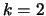 .
.
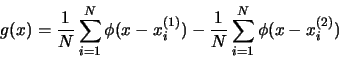

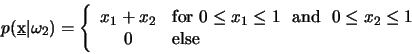
![$ \left[\begin{array}{c} 0 0 \end{array} \right]
\left[\begin{array}{c} 1 1 \end{array} \right]
\left[\begin{array}{c} 2 1 \end{array} \right] $](img51.gif) The samples from class 2 are:
The samples from class 2 are:
![$ \left[ \begin{array}{c} 1 0
\end{array} \right] \left[ \begin{array}{c} 1 ...
... -1 \end{array} \right] \left[
\begin{array}{c} 1 -2 \end{array} \right]$](img52.gif) Sketch the 1-NN
class boundaries for the this set of sample points.
Sketch the 1-NN
class boundaries for the this set of sample points.