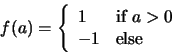Next: EEL6825: Projects
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#4
Get PDF file
Due Wednesday, November 14, 2001 in class. Late homework will be penalized as usual but will not be accepted
after class starts on 11/16 since Exam II is 11/19.
PART A: Textbook Problems Answer the following questions,
you should not need a computer.
- A1
- Class
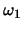 points are:
points are:
Class 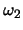 points are:
points are:
Find any weight vector 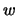 such that
such that 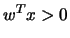 for all class
for all class 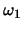 points and
points and 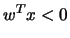 for all class
for all class 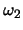 points. Justify your answer.
points. Justify your answer.
- A2
- Using the points in [A1] as the training set, classify
![$[1,1,1]^T$](img59.gif) using 3-Nearest Neighbor voting.
using 3-Nearest Neighbor voting.
- A3
- i
- Under what conditions does the K-L dimensionality reduction
technique fail miserably (huge increase in classification error when the dimensionality is reduced)
- ii
- Under what conditions does it
perform wonderfully (guaranteed no change in classification error when the dimensionality is reduced).
- A4
- Compare and contrast Bayes classifiers, nearest neighbor classifiers and neural network classifiers in
terms of computation time required for (i) training and (ii) classification.
- A5
- Two normal distributions are characterized by:
If you could only keep one of the four original features ( or
or 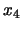 ), which one would you keep for
lowest classification error? Explain.
), which one would you keep for
lowest classification error? Explain.
PART B: KL Transform.
Two normal distributions are characterized by:
Answer the following questions regarding the KL dimensionality reduction of this problem. Show all of your work. If
you use a computer, use it only to check your work. Do not turn in any computer results for this problem.
- B1
- Compute the combined covariance matrix
(
 ) of the data. Remember that the combined distribution of two equally likely
normal distributions is not a normal distribution but the combined covariance matrix can be expressed as:
) of the data. Remember that the combined distribution of two equally likely
normal distributions is not a normal distribution but the combined covariance matrix can be expressed as:
- B2
- Compute the normalized eigenvectors and their respective eigenvalues.
- B3
- If you had to drop a single feature, which feature would it be? What is the error that you would then pay in terms
of representation and in terms of classifier performance?
- B4
- Map the two distributions to the new two-dimensional space spanned by
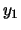 and
and 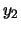 . What are the new values of
the 2-dimensional
. What are the new values of
the 2-dimensional
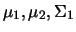 and
and 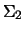 ? Sketch the new 2D problem.
? Sketch the new 2D problem.
- B5
- What is the mean of the two 2-dimensional covariance matrices? Is there any significance to its value?
PART C: Neural Networks
Consider the following sample points: The samples from class 1 are:
![$ \left[ \begin{array}{c} 0 0 \end{array}
\right] \left[ \begin{array}{c} 1 2 \end{array} \right] \left[\begin{array}{c} -1 2 \end{array} \right] $](img70.gif) The
samples from class 2 are:
The
samples from class 2 are:
![$ \left[ \begin{array}{c} 0 1
\end{array}\right] \left[ \begin{array}{c} 1 -1
\end{array} \right] \left[
\begin{array}{c} -1 -1 \end{array} \right]
$](img71.gif) Answer the following questions regarding the multilayer perceptron solution to this problem.
Answer the following questions regarding the multilayer perceptron solution to this problem.
- C1
- What is the minimum number of hidden units that can solve this problem? Is your answer different if you use smooth
sigmoid functions vs. hard-limiting functions? Explain.
- C2
- Assume the sigmoid activation function of the neural network to be:
Derive a neural network architecture that solves this problem. The final output of your neural network should be +1
for class 1 and -1 for class 2. Provide all of the necessary weight values for architecture with the minimum number
of hidden units. Sketch a plot that shows the region boundaries. Explain your reasoning and justify your results.
- C3
- Run a backpropagation algorithm to solve this problem with the minimum number of hidden units
you answered in [C1].
You are strongly recommended to use the matlab neural network toolbox that
was discussed in class but you are free to use whatever software you like
or even to program your own. Use the same architecture that you came up
with in [C2] only do not use a hard-limiting nonlinear function. Show a few plots of MSE vs.
epoch. Does the network find the same (or similar) solution to what you listed in [C2]? How frequently (if ever) does your
network get trapped in local minima?
- C4
- Explore the effect on accuracy and convergence rate when you use 1, 2, 3, 4, and 5 hidden units
from for this problem. Show an example of the region boundaries for each case. Comment on your results.
- C5
- Hand in a plot of the decision boundaries for class 1 and
class 2 along with the data points. There should be no errors. Note: it
may be helpful for you to periodically plot these regions as the algorithm
is running to see how far you are away from the correct solution.



Next: EEL6825: Projects
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#4
Dr John Harris
2001-11-26
![\begin{displaymath}
\left[
\begin{array}{c}
-1 \\
-1 \\
+1
\end{array}
...
...[
\begin{array}{c}
+1 \\
-1 \\
-1
\end{array}
\right]
\end{displaymath}](img54.gif)
![\begin{displaymath}
\left[
\begin{array}{c}
+1 \\
+1 \\
-1
\end{array}
...
...[
\begin{array}{c}
-1 \\
+1 \\
+1
\end{array}
\right]
\end{displaymath}](img55.gif)
![\begin{displaymath}\mu_1=
\left[
\begin{array}{c}
0 \\
0 \\
0 \\
0
\en...
... \\
0&1&0&0 \\
0&0&1&0 \\
0&0&0&3
\end{array}
\right]
\end{displaymath}](img60.gif)
![\begin{displaymath}\mu_1=\mu_2=
\left[
\begin{array}{c}
0 \\
0 \\
0
\end...
...rray}{ccc}
5&0&4 \\
0&5&4 \\
4&4&4
\end{array}
\right]
\end{displaymath}](img63.gif)
![$ \left[ \begin{array}{c} 0 0 \end{array}
\right] \left[ \begin{array}{c} 1 2 \end{array} \right] \left[\begin{array}{c} -1 2 \end{array} \right] $](img70.gif) The
samples from class 2 are:
The
samples from class 2 are:
![$ \left[ \begin{array}{c} 0 1
\end{array}\right] \left[ \begin{array}{c} 1 -1
\end{array} \right] \left[
\begin{array}{c} -1 -1 \end{array} \right]
$](img71.gif) Answer the following questions regarding the multilayer perceptron solution to this problem.
Answer the following questions regarding the multilayer perceptron solution to this problem.