


Next: EEL6825: HW#4
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#2
Get PDF file
Part A is due on Friday, September 28 in class. No credit for
late turn in since we will go over part A in class. Part B is due
Friday, October 5, 2001 in class. Late part B will lose
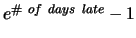 percentage points. Click on
http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
to see the current penalty.
PART A: Textbook Problems Answer the following questions,
you should not use a computer but certainly can use one to check
your work.
percentage points. Click on
http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
to see the current penalty.
PART A: Textbook Problems Answer the following questions,
you should not use a computer but certainly can use one to check
your work.
- A1
- (a)
- Is it possible for the Bhattacharrya bound to be less than the Bayes
error? Assume that you are given the exact distributions, parameters
and a priori probabilities. Explain why or why not.
- (b)
- Is it possible for the Bhattacharrya bound to be greater than 1/2 for a
two-class classification problem? Explain why or why not.
- A2
- Find a discriminant function
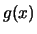 that successfully classifies the
following data points. Class
that successfully classifies the
following data points. Class 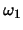 points are given by:
points are given by:
Class 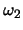 points are given by:
points are given by:
- A3
- Given sampled data points, a student found that a linear
classifier outperformed the Bayes classifier. Since she correctly
assumed that the data was generated by Normal distributions, what
probably was the explanation? (The Bayes classifier is supposed
to be optimal!)
- A4
- Given the following data points, find the w vector that minimizes
the Fisher criterion. Assume
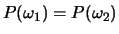 . Make sure that you
normalize w and that it points in the proper direction.
Justify your answer.
Class
. Make sure that you
normalize w and that it points in the proper direction.
Justify your answer.
Class 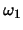 points are given by:
points are given by:
Class 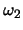 points are given by:
points are given by:
- A5
- Given the following data points, find the w vector that minimizes
the Fisher criterion. Assume
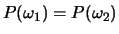 . Make sure that you
normalize w and that it points in the proper direction.
Justify your answer.
Class
. Make sure that you
normalize w and that it points in the proper direction.
Justify your answer.
Class 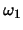 points are given by:
points are given by:
Class 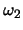 points are given by:
points are given by:
PART B: Computer Experiment: Mines and rocks with linear
classifiers
The programming part of this assignment uses the data set
developed by Gorman and Sejnowski in their study of the
classification of sonar signals using a neural network. The task
is to train a network to discriminate between sonar signals
bounced off a metal cylinder and those bounced off a roughly
cylindrical rock.
The file ``mines.asc''
(http://www.cnel.ufl.edu/hybrid/courses/EEL6825/mines.asc)
contains 111 patterns obtained by bouncing sonar signals off a
metal cylinder at various angles and under various conditions. The
file ``rocks.asc''
(http://www.cnel.ufl.edu/hybrid/courses/EEL6825/rocks.asc)
contains 97 patterns obtained from rocks under similar conditions.
The transmitted sonar signal is a frequency-modulated chirp,
rising in amplitude. The data set contains signals obtained from
a variety of different aspect angles, spanning 90 degrees for the
cylinder and 180 degrees for the rock. Each pattern is a set of
60 numbers in the range 0.0 to 1.0. Each number represents the
energy within a particular frequency band, integrated over a
certain period of time. The integration aperture for higher
frequencies occur later in time, since these frequencies are
transmitted later during the chirp. A
README.txt
file in the directory contains a longer description of the data
and past experiments.
For part B, assume that the a priori probabilities of each class
are approximated by the respective fractions of each class in the
data samples.
- B1
- Show several (e.g. 3) 2D scatter plots of the data showing only
two features at a time. Do any of the plots show the data to be
linearly separable? Can you infer anything about the linear
separability of the overall data set from these 2D plots (or from
all possible 2D plots)? Explain.
- B2
- Use the Fisher criterion to compute the ``optimal'' w
vector. What is the the numerical value of the normalized w vector?
- B3
- Show an informative plot of the data points from both classes projected onto
this one dimension. Think carefully how best to show this
information.
- B4
- Have your program do a linear search for the optimal
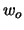 value.
What value of
value.
What value of 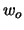 do you find?
do you find?
- B5
- What is the resulting classification error for your Fisher
classifier (resubstitution)?



Next: EEL6825: HW#4
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#2
Dr John Harris
2001-11-26
![\begin{displaymath}
\left[ \begin{array}{c} 0 0 \end{array} \right] \left[
\begin{array}{c} 1 1 \end{array} \right]
\end{displaymath}](img32.gif)
![\begin{displaymath}
\left[ \begin{array}{c} 0 1 \end{array} \right] \left[
\begin{array}{c} 1 0 \end{array} \right]
\end{displaymath}](img33.gif)
![\begin{displaymath}
\left[\begin{array}{c} 0 0 \end{array} \right]
\left[\b...
...y} \right]
\left[\begin{array}{c} 1 2 \end{array} \right]
\end{displaymath}](img35.gif)
![\begin{displaymath}
\left[ \begin{array}{c} 1 0 \end{array} \right] \left[
...
...\right]
\left[
\begin{array}{c} 2 2 \end{array}
\right]
\end{displaymath}](img36.gif)
![\begin{displaymath}
\left[ \begin{array}{c} 0 0 \end{array} \right] \left[
\begin{array}{c} 0 1 \end{array} \right]
\end{displaymath}](img37.gif)
![\begin{displaymath}
\left[ \begin{array}{c} 1 0 \end{array} \right] \left[
\begin{array}{c} 1 1 \end{array} \right]
\end{displaymath}](img38.gif)