EEL6825: HW#2

EEL 6825  -  Fall 1997

Due Friday, September 19, 1997 at 3pm. Do not be late to class.

1. Problem 2-5 in D&H
2. Do not use Matlab for this problem. (Of course you may use any method you like to check your work.) Two normal distributions are characterized by:

   

   

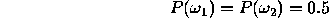
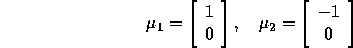
   Derive the analytic form and sketch the Bayes decision boundary for the following cases: (Also sketch some equi-probability contours for each distribution.)

   1. 

   2. 

   3. 

      

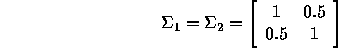
3. You must use Matlab to solve this problem. Consider once again problem 2c.
   1. Plot 100 samples from each class on a graph. The Matlab randn() function generates samples from a unit normal distribution.
   2. Check that your samples are reasonable by computing the sampled mean and sampled covariance matrix (mean() and cov() in Matlab).
   3. Graph the Bayes decision boundary on the plot. This boundary reflects the optimal decision function and requires knowledge of the original distributions not the values of the random samples. How many samples are incorrectly classified? Run your program many times with different sets of data and report the average, standard deviation, and the number of trials you ran.
   4. Hand in one plot from Matlab showing equi-probability contours and one set of samples from each class. (You may draw the equi-probability contours by hand if you don't know how to do this in Matlab.)
   5. Draw the Bayes decision surface on your plot (by hand only if you can't figure out how to do it in Matlab). Circle the misclassified points.

   (turn over)

4. Compute an upper bound for the Bayes error using the Bhattacharyya bound. An analytical expression for the Bhattacharyya bound can be found by evaluating the integral derived in problem 1. Solving the integral for Normal distributions gives an upper bound on the error of:

   

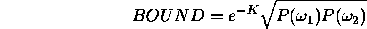
   where K is given by:

   

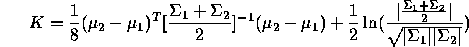
   This equation can be found on page 99 of Fukanaga if you want to read more about it. However all of the information you need is provided above.

5. For extra credit, compute the exact Bayes error for the problem in 2c given the known distributions.

Final notes:

• Your homework should be in two distint parts. Part 1 should show the answers, plots, hand calculations etc. that you need to answer the questions. Part 2 should contain all of the Matlab code that you have writen to generate the answers in the first part.
• During the homework assignments, some amount of communication between students is fine and even encouraged. However, the final solutions and all the code that you turn in should be your own.
• You do not necessarily need to use Matlab, you can use any computer language you like as long as you can perform the equivalent compuations.
• Good luck!