EEL6825: HW#3

EEL 6825  -  Fall 1997

Due Monday, October 6, 1997 at 3pm. Do not be late to class.

PART A: Non-computer questions

A1

Problem 3-2 in D&H

A2

Problem 3-4 in D&H

A3

In completing an assignment, a student generated 100 samples from two given Normal distributions. She was surprised to discover that the classification error on the samples was larger than the Bhattacharyya bound she computed from the given distribution parameters! Since the Bhattacharyya bound is supposed to be an upper bound on the Bayes error, can you explain her results?

A4

Is it possible for a linear classifier to have an expected classification error that is less than the Bayes error? Why or why not?

A5

Problem 3.2 in Bishop

PART B: Bayes Classifier with 3 classes

You are given the heights and weights of all of the players in the WNBA (Women's National Basketball Association) at the end of last season. The file can be found in
http://www.cnel.ufl.edu/analog/courses/EEL6825/wnba.asc Each line of the file consists of four numbers: (1) Player's position. 1=guard 2=forward 3=center. (Guards are usually smaller than forwards who are usually smaller than centers.) (2) Player's height: truncated value in feet (3) Player's height - truncated value: in inches (4) Player's weight: pounds.

B1

Read in the data and print a scatter plot showing the three different classes with height on the 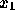axis and weight on the 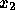axis. Are any two of the classes linearly separable?

B2

Compute the sampled mean and covariance matrix for each position.

B3

Assume that all three classes are generated from normal distributions with equal a priori probabilities. Design a Bayes classifier using the sampled mean and covariance matrix. Draw the discriminant boundaries on the scatter plots. How many players are classified incorrectly?

B4

Can you draw two linear boundaries by hand that classify better than the sampled Bayes Classifier?

B5

What position would you play if you played in the WNBA?

PART C: Bayes Classifiers vs Linear Classifiers

You can find the data for the heights and weights of all of the players in the Eastern Conference of the NBA at: http://www.cnel.ufl.edu/analog/courses/EEL6825/nba.asc The format is the same as for that in Part B. In this part of the homework, however, we are only interested in classifying people as players in the WNBA or NBA using their height and weight values.

C1

Compute the sampled mean and covariance matrix for each class.

C2

Derive a Bayes classifier assuming that the two a priori probabilities correspond to the composition of the data set. Show the decision boundary on the plot. How many points are classified incorrectly?

C3

Compute the Bhattacharyya bound. How does this value correspond to the number of misclassified points?

C3

Derive the direction for Fisher's linear discriminant. What are the components of the w vector? Compute an optimal threshold by scanning through all of the data points. What is the value of your threshold?

C5

Draw the decision boundary on a scatter plot. How many points are misclassified?