EEL6825: HW#1

Due Friday, September 5, 1997 at 3pm. Do not be late to class.

1. Problem 1.9 in Bishop.
2. Problem 1.10 in Bishop.
3. You are given two one-dimensional distributions. for and 0 otherwise. for and 0 otherwise. Assume that .
   1. Derive the Bayes decision rule for this two-class classification problem. That is, you should specify how all values of x should be classified for minimum error.
   2. Compute the Bayes error.
4. Three one-dimensional distributions are given as uniform in [-1/3,1/3] for , uniform in [-1/2,1/2] for and uniform in [-1,1] for . .
   1. Compute 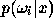for each class and sketch each function on a separate plot.
   2. Consider a Bayes classifier for the three distributions. Be sure to describe the class for each possible value of x.
   3. Compute the Bayes error.
5. In many pattern classification problems one has the option either to assign the pattern to one of c classes or to reject it as being unrecognizable. If the costs for rejects is not too high, rejection may be a desirable action. Let

   

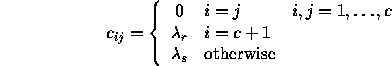
   where is the loss incurred for choosing the (c+1)th action of rejection, and is the loss incurred for making a substitution error. Show that the minimum risk is obtainable if we decide if for all j and if and reject otherwise. What happens if ? What happens if ?