EEL6825: HW#3

Due Thursday, October 3, 1996 at 3pm. As usual hand in all code that you write

1. Answer each of the following with a short statement, derivation and/or sketch.
   1. A certain linear classifier ( 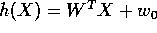) gives an error of 55% on a two-category classification problem. Explain the simplest way of improving the performance of this classifier on the test data.
   2. Is it possible for a linear classifier to have an expected classification error that is less than the Bayes error? Why or why not?
   3. In completing an assignment, a student generated 100 samples from two given Normal distributions. She was surprised to discover that the classification error on the samples was larger than the Bhattacharyya bound she computed from the given distribution parameters! Since the Bhattacharyya bound is supposed to be an upper bound on the Bayes error, can you explain her results?
2. Suppose you are given data as Suppose the first 3 are labeled and the remaining 4 are labeled .
   • Sketch the decision boundary resulting from using the nearest-neighbor rule for classification.
   • Find the sampled mean for each class and sketch the decision boundary corresponding to classifying X by assigning it to the category of the nearest sample mean.
3. Two one-dimensional distributions are given as uniform in [0,1] for and uniform in [0,2] for . Assuming that and that an infinite number of samples is available
   1. Compute the Bayes error.
   2. Compute the expected probability of error for the 1-NN leave-one-out procedure.
   3. Compute the expected probability of error for the 2-NN leave-one-out procedure. Do not include the sample being classified and assume that ties are rejected.
   4. Explain why the 2-NN error computed in part 3 is less than the Bayes error. Note that you can and should still answer this part even if you didn't get the above parts correct.

   (turn over)

4. Generate 100 points of data from a distribution with and Compute the mean and covariance of your test data to see if you did everything right. Show a scatter plot of the result. Some hints:
   • If you are using MATLAB, the randn() function generates samples from a unit normal distribution.
   • One method of creating the class2 samples is by using the whitening transform as described in class.

     

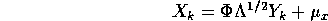
     You will probably need to use the eig() function in MATLAB.

5. Generate N (you will be told the value of N later) 8-dimensional data points from each of two normal distribution with the following parameters: and
   and Once you generate the data, you should forget the actual parameters that you used to generate the distributions. All you can use is the data to generate the following 3 classifiers:
   1. Linear classifier - any version you like, probably the easiest is to assume that the data comes from Gaussian distributions with equal covariance matrices.
   2. Quadratic classifier - using the same program you wrote from HW#2
   3. Nearest-neighbor classifier
   Run each classifier on at least 10 different sets of data samples. List the mean and standard deviation of the error for each classifier for both the resubstitution and hold-out methods. The complete answer includes 12 numbers: (3 classifiers x 2 design methods (R and H) x 2 measures (mean and ) = 12 numbers) For the Hold-out method split your data exactly into half and use one half for test and the other half for training. As you already know from class, for Resubstitution, you will use all N samples for both test and training. Make sure that you hand in all of the code you write.
6. Extra Credit Implement the Leave-one-out method and compute the mean and standard deviation of your error estimate as you did in the last problem. How do you results compare to the resubstitution and hold-out results you computed?