EEL6825: HW#2

Due Thursday, September 19, 1996 at 3pm. All of the computer code you write to generate any of the answers on homework should always be turned in with your homework solution.

1. Let x have an exponential distribution given by

   

   and for x<0.

   1. Sketch 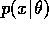versus x for a fixed value of the parameter .
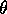   2. Sketch 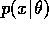versus 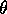( a fixed value of x.
   3. Suppose that N samples are drawn independently according to 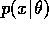. Give an equation for the maximum likelihood estimate for .
2. Answer each of the following with a short statement, derivation and/or sketch.
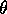   1. If x is a 1D random variable given by a normal distribution with mean 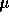and variance 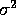, what is ?
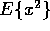   2. It is well known that if two normal distributions have the same covariance matrix, the Bayes discrimination function is linear. However, given two non-normal probability distributions are identical, except for their means, is the Bayes classifier necessarily linear? Why or why not?
   3. You are given data drawn from two Normal distributions. It turns out that the data points are linearly separable. Is the Bayes Classifier you design guaranteed to correctly classify all of the data points?

3. The rest of this homework explores the well known Iris Data Set. This data set was published by Fisher (1936) and has been used widely as a testbed for statistical analysis techniques. Fisher's paper is a classic in the field and is referenced frequently to this day. The sepal length, sepal width, petal length, and petal width were measured on 50 iris specimens from each of 3 species, Iris setosa, Iris versicolor, and Iris virginica. This is perhaps the best known database to be found in the pattern recognition literature. The data are listed on page 342 of N&S but are also available through anonymous ftp through jupiter.cnel.ufl.edu. Directory eel6825/hw2 contains three ascii files entitled setosa.asc, versicolor.asc and virginica.asc. Copy these to your directory. The files may be read into matlab with the load command using the -ascii option.
   1. Compute the mean and covariance matrices for each class. (Make sure you get the same results as those given on page 343 in the N&S.)
   2. Plot the three classes on the same plot using only two dimensions at a time. Can you show that one or more classes linearly separable from the other classes using just two of the dimensions? Hand in only the best plot that illustrates your answer.
   3. Assume that the classes are generated from normal distributions with equal a priori probabilities. Use the sampled mean and sampled covariance matrix of each class to design a Bayes classifier. Indicate on a plot which points are misclassified. Hand in all of your code.
   4. Compute the Bhattacharrya bound on the Bayes error. How does it compare to the actual error you found?
   5. Extra Credit: Show the Bayes discriminant surfaces in this 2D space (i.e. the curves should appear on the plot). Your code should be written in a general fashion so that no part needs to be changed if new data is provided.