EEL6825: HW#4

Due Thursday, November 7, 1996 at 3pm. As usual hand in all code that you write

This assignment is a simplified introduction to speech recognition.

Part A: Getting the data

A1

Record yourself and at least two others speaking five vowel sounds, (short a, long e, long i, long o, long u). Break your data into a test and training set. If you would rather, you may use only one speaker but record at least three different times-this makes the classification much easier but less interesting. You can record using any system you want-feel free to team up with other people to record and share the data. Read the note about the shareware program called goldwave in the next paragraph. Note, if you absolutely, absolutely are not able to record data :( ftp the data in http://www.cnel.ufl.edu/analog/courses/EEL6825. There are 3 data sets there from three speakers. The first letter indicates the speaker and the second indicates the vowel. So for example, ``me.mat'' indicates speaker M and vowel ``e''. Speakers J and S are male and M is female. Everyone is strongly encouraged to record some data and discover the issues involved. You can combine data you recorded with the the ftp-ed data if you like. Fully explain how you obtained your data (what programs, sampling rates, who the speakers were, etc.)

Goldwave is a shareware program that you can get from http://www.shareware.com and search for goldwave. http://www.cnel.ufl.edu/analog/courses/EEL6825 also contains a copy (gwave322.zip). You have to unzip this file and store it in a directory on your PC. To record, select ``new'' and choose 16-bit, 22050 Hz sampling, and choose a 1 second recording time. Press the red record button and speak into the microphone. Once you recorded one vowel in the one second interval, save it as a MATLAB .mat file.

A2

Plot a zoom up of some of the vowels in the training set showing only 5 or so periods of each signal. An example is shown below (left) without proper numbering or labeling on the axes.

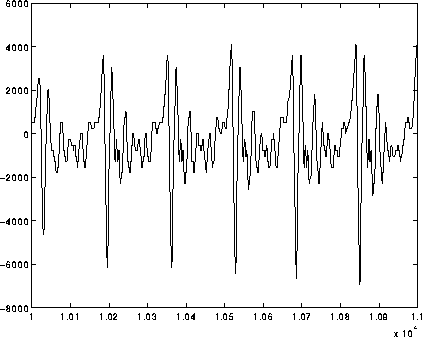
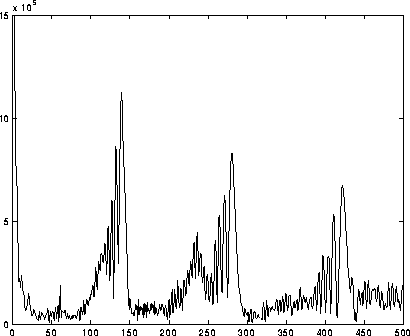
A3

Perform an fft of each signal. Plot the magnitude of the fft of each vowel being sure to zoom up on the frequencies of interest and showing the real frequencies on the x-axis. An example is above (right), again without proper numbering and labeling of the axes

Part B: Creating the feature vector

B1

Now we are ready to build your feature vector. Using the results from the fft from Part A, choose carefully the frequency range that you want to include in your feature vector. Also choose carefully the sampling resolution that you require. For example you could subsample the vector by averaging the magnitudes for each group of 10 or some other number of frequencies. Normalize each resulting vector by dividing by its maximum value. Create these feature vectors for each pattern you have in the test and training sets.

B2

Build a classifier, probably 1-NN is the simplest. Be careful not to use the test data in designing your classifier. What is the performance of your classifier on the test data?

Part C: K-L transform

C1

Run a K-L transform on all of the training data.

C2

Choose a reduced number of features from the K-L transform and explain how you decide which features to keep.

C3

What is the performance on the new classifier on the test data? Remember you must perform exactly the identical transformation on your test data as your training data (i.e., don't take the K-L transform of your test data!)

Note: each of you must use the K-L or other dimensionality reduction program for your final project. If you are clever, you can write your code so you can use it for both purposes without modification.

Part C: Short questions

D1

Explain how the classification in this assignment is achieved independent of the intensity of the sounds.

D2

Discuss an alternative feature vector you could have used for this assignment, i.e. not using the Fourier transform. Would you expect this feature to work better?

D3

The density function of a two-dimensional random vector x consists of four impulses at (0,3) (0,1) (1,0) and (3,0) with probability of 1/4 for each. Find the K-L expansion. Compute the mean-square error when one feature is eliminate. Compute the contribution of each point to the mean-square error.

D4

Suppose a student is given data that consists of many 2-D samples of the 1-D curve described by: where 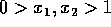. Why can't the standard K-L transform accurately represent this data in one dimension? Sketch the likely result of using the K-L transform to reduce the dimension for this problem.