EEL6825: HW#1

Due Thursday, September 5, 1996 at 3pm. You do not need to use a computer for any of the questions.

1. Three one-dimensional distributions are given as uniform in [-1/3,1/3] for , uniform in [-1/2,1/2] for and uniform in [-1,1] for . .
   1. Compute 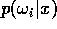for each class and sketch each function on a separate plot.
   2. Implement a Bayes classifier for the three distributions. Be sure to describe the class for each possible value of x.
   3. Compute the Bayes error.
2. You don't need to use a computer for this problem. Two normal distributions are characterized by:

   

   

   Derive the analytic form and sketch the Bayes decision boundary for the following cases: (Also sketch some equi-probability contours for each distribution.)

   1. 

   2. 

      

   3. 

      

   (turn over)

3. In many pattern classification problems one has the option either to assign the pattern to one of c classes or to reject it as being unrecognizable. If the costs for rejects is not too high, rejection may be a desirable action. Let

   

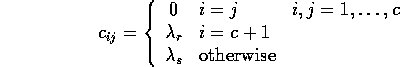
   where is the loss incurred for choosing the (c+1)th action of rejection, and is the loss incurred for making a substitution error. Show that the minimum risk is obtainable if we decide if for all j and if and reject otherwise. What happens if ? What happens if ?

4. EXTRA CREDIT
   You are give two 1D normal probability distributions as ( ): and . Assume .
   • Describe the complete Bayes Decision rule (i.e. describe how you would classify each possible value of x).
   • Compute the Bayes error (you may need to do this numerically)