


Next: EEL6825: HW#4
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#2
Due Friday, October 20, 2000 in class. Late
homework will lose
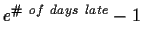 percentage points.
To see the current late penalty, click on
percentage points.
To see the current late penalty, click on
http://www.cnel.ufl.edu/analog/harris/latepoints.html
PART A: Textbook Problems
Answer the following questions, you should not use a computer.
- A1
- You are given two one-dimensional data points. One occurs
at +1 and the other at -1.
- (a)
- Derive the formula and sketch the Parzen windows estimate
of the pdf for h=1.5.
- (b)
- Derive the formula and sketch the Parzen windows estimate
of the pdf for h=3.0.
- (c)
- Derive the formula and sketch the k-NN estimate
of the pdf for k=1.
- (d)
- Derive the formula and sketch the k-NN estimate
of the pdf for k=2.
- A2
- Assuming that
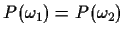 and that you are given
N data points from each of two classes.
The Parzen classifier is expressed by
and that you are given
N data points from each of two classes.
The Parzen classifier is expressed by
where the superscripts denote the class of each data point.
Prove that the leave-one-out error is larger than the resubstitution
error. Assume that
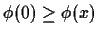 .
.
- A3
- You are given the following two 1-D distributions:
Assume that
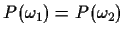 and a large number of
samples is available. Answer the following questions:
and a large number of
samples is available. Answer the following questions:
- (a)
- Compute the expected probability of error for the 1-NN resubstitution
procedure.
- (b)
- Compute the expected probability of error for the 1-NN leave-one-out
procedure.
- (c)
- Compute the expected probability of error for the 2-NN leave-one-out
procedure. Do not include the sample being classified and assume that
ties are rejected.
- (d)
- Explain why the 2-NN error computed in part (c) is less than the Bayes
error.
- A4
- Consider the following sample points:
The samples from class 1 are:
![$
\left[ \begin{array}{c} 0 \\ 0 \end{array} \right]
\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]
$](img37.gif) The samples from class 2 are:
The samples from class 2 are:
![$
\left[ \begin{array}{c} 1 \\ 0 \end{array} \right]
\left[ \begin{array}{c} 1 \\ -1 \end{array} \right]
$](img38.gif) Sketch the 1-NN class boundaries for the this set of sample points.
Sketch the 1-NN class boundaries for the this set of sample points.
- A5
- For the same points as in A4, sketch the 2-NN class boundaries for
the above set of sample points. Make sure you indicate the reject region.
PART B: Computer Experiment: Mines and rocks with linear classifiers
The programming parts of this assignment uses the data set developed by
Gorman and Sejnowski in their study of the classification of sonar signals
using a neural network. The task is to train a network to discriminate
between sonar signals bounced off a metal cylinder and those bounced off a
roughly cylindrical rock.
The file ``mines.asc''
(http://www.cnel.ufl.edu/analog/courses/EEL6825/mines.asc)
contains 111 patterns obtained by bouncing sonar signals off a metal
cylinder at various angles and under various conditions. The file
``rocks.asc''
(http://www.cnel.ufl.edu/analog/courses/EEL6825/rocks.asc)
contains 97 patterns obtained from rocks under similar
conditions. The transmitted sonar signal is a frequency-modulated chirp,
rising in amplitude. The data set contains signals obtained from a variety
of different aspect angles, spanning 90 degrees for the cylinder and 180
degrees for the rock. Each pattern is a set of 60 numbers in the range 0.0
to 1.0. Each number represents the energy within a particular frequency
band, integrated over a certain period of time. The integration aperture
for higher frequencies occur later in time, since these frequencies are
transmitted later during the chirp. A
README.txt
file in the directory contains
a longer description of the data and past experiments.
For parts B and C, assume that the a priori probabilities of each class are
approximated by the respective fractions of each class in the data samples.
- B1
- Use the Fisher criterion to compute the ``optimal'' w
vector. Show a plot the data points from both classes
projected into this one dimension.
- B2
- Have your program do a linear search for the optimal wo value.
What value of wo do you find. What is the resulting classification
error for your Fisher classifier (resubstitution)?
PART C: Computer Experiment: Mines and rocks with nearest neighbor classifier
- C1
- Design a nearest-neighbor classifier that chooses the class of the
nearest-neighbor for each point. Compute the resubstitution and the
leave-one-out errors. Clearly indicate these results in your answers.
Programming hint: Do not use all of the data points when you are
developing your code. When you are confident that your program is
correct, run with the full number of points. Also, write your code with
efficiency in mind. If the full number of points still takes too long to
run, use as many points as you think reasonable but explain what you have
done.
- C2
- Plot a graph that shows the leave-one-out performance of your
classifier that on a d2 display like we discussed in class. The Y-axis
represents the distance between each point in the data set and its nearest
neighbor in the mines class. If the data point happens to come from the
mines class, leave it out of the minimum distance computation. Similarly,
the X-axis is the distance between each data point and its nearest
neighbor in the rocks class. (None of the distances should be exactly
zero since you are using the leave-one-out method and no points are
exactly repeated.) Plot a line on the plot that shows your solution to
problem C1.
As usual, include all plots and answers to questions in the first part of
your document. All matlab code that you write should be included in the
second part.



Next: EEL6825: HW#4
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#2
Dr John Harris
2000-12-03
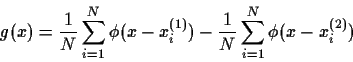

![$
\left[ \begin{array}{c} 0 \\ 0 \end{array} \right]
\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]
$](img37.gif) The samples from class 2 are:
The samples from class 2 are:
![$
\left[ \begin{array}{c} 1 \\ 0 \end{array} \right]
\left[ \begin{array}{c} 1 \\ -1 \end{array} \right]
$](img38.gif) Sketch the 1-NN class boundaries for the this set of sample points.
Sketch the 1-NN class boundaries for the this set of sample points.