


Next: EEL6825: HW#3
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#1
Due Friday, September 22, 2000 in class. Late
homework will lose
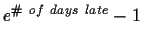 percentage points.
See http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
for the current penalty.
percentage points.
See http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
for the current penalty.
Your homework should be in two distinct sections. The first section should
show the answers, explanations, plots, hand calculations etc. that you need
to answer the questions in parts A-C. The second section should contain all
of the Matlab code that you have written to generate the answers in the
first section. You don't need a computer for parts A and B but of course you
may use one to check your work if you like.
PART A: Short Answer Questions
- A1
- (5 points)
You are given the heights and weights of a certain set of
individuals in unknown units. Which one of the following six matrices is
the most likely to be the sampled covariance matrix? Explain your reasoning.
1.232 0.013 1.232 0.867 1.232 -0.867
0.013 2.791 -0.867 2.791 -0.867 3.307
1.232 3.307 1.232 0.867 1.232 3.307
0.013 2.791 0.867 2.791 3.307 2.791
- A2
- (5 points)
Is it possible for the Bhattacharrya bound to be greater than 1/2 for a
two-class classification problem? Explain why or why not.
- A3
- (5 points)
Sample data from one class are given as:
Compute the sampled mean and sampled covariance matrix (by hand). Make
sure to use estimators that are unbiased. Show your work.
- A4
- (5 points) The random variable x follows the Erlang pdf:
where u(x) is the unit step function. Derive the maximum
likelihood estimate of 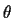 given N measurements
given N measurements
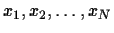 .
.
- A5
- (5 points)
How does the Bayes error change when a simultaneous diagonalization is
performed (i.e.increase, decrease, stay the same or other)? Assume the
distributions are normal in d-dimensional space.
(turn over)
PART B: Maximum Likelihood Problem
Consider the following probability distribution:
- B1
- (5 points)
For what values of k is this distribution valid?
Verify that this distribution integrates to one for all valid values of k.
- B2
- (15 points)
Given N data points
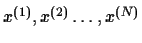 sampled from a
distribution, derive a
formula for the maximum likelihood value of k for the distribution.
sampled from a
distribution, derive a
formula for the maximum likelihood value of k for the distribution.
- B3
- (5 points)
Suppose N=3 and
x(1)=e0=1,
x(2)=e-1,
x(3)=e-2. What the numerical
value of the maximum likelihood estimate of k?
PART C: Computer Experiment: Bayes Classifier with two classes
Two normal distributions are characterized by:
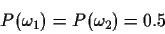
![\begin{displaymath}\mu_1=
\left[
\begin{array}{c}
0 \\
0
\end{array}\right]
,
\...
...\left[
\begin{array}{cc}
.2&-.1 \\
-.1&.2
\end{array}\right]
\end{displaymath}](img30.gif)
- C1
- (5 points) Generate 200 points from each of these distributions. Show a scatter plot
of the data using two different symbols (and colors) to identify the classes.
- C2
- (5 points) Compute the sampled mean and covariance matrix for each class.
How close are these values to the true mean and covariance matrix?
- C3
- (20 points) Write a matlab program that classifies the data using a Bayes
Classifier. Assume the data comes from Normal distributions but use your
estimated parameters in the classifier. What is the percent error that
you find? Run your program several times and average your results to improve your estimate of the expected error.
- C4
- (10 points) Compute the Bhatacharrya bound for this problem can compare to your
actual error from [C3]. Remember from class that the Bhatacharrya bound is an upper bound on the expected Bayes error for
Normal distributions and is given by:
where K is given by:
Again use the estimated parameters in your calculation.
- C5
- (10 points) Have the computer draw the decision surface on
the scatter plot. (Do not hard code the particular boundary for
this problem, you should write a general program.) Hint: think
about using the functions meshgrid and contour in matlab.



Next: EEL6825: HW#3
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#1
Dr John Harris
2000-12-03
![\begin{displaymath}\left[ \begin{array}{c} 1 \\ 2 \end{array} \right]
\left[ \be...
...} \right]
\left[ \begin{array}{c} -1 \\ -2 \end{array} \right]
\end{displaymath}](img24.gif)
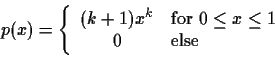
![\begin{displaymath}\mu_1=
\left[
\begin{array}{c}
0 \\
0
\end{array}\right]
,
\...
...\left[
\begin{array}{cc}
.2&-.1 \\
-.1&.2
\end{array}\right]
\end{displaymath}](img30.gif)
![\begin{displaymath}K=\frac{1}{8}(\mu_2-\mu_1)^T[\frac{\Sigma_1+\Sigma_2}{2}]^{-1...
...igma_2}{2}\vert}{\sqrt{\vert\Sigma_1\vert\vert\Sigma_2\vert}})
\end{displaymath}](img32.gif)