EEL6586: HW#2

Due Monday, Feb 22, 1999 in class. Late homework will lose $e^{\char93 ~of~days~late} -1$ percentage points. To see the current late penalty, click on
http://www.cnel.ufl.edu/analog/harris/latepoints.html Note: We will have an in-class exam on Friday, Feb 26.

Noncomputer Problems:

1.

Problem 4.5 in DPH

2.

figure=/home/harris/courses/6586/hw2/prob1.ps,height=2.5in

Consider the infinite-length signal x(n), a short segment is shown above. Your goal is to derive the LPC coefficients for the prediction of x(n). Assume order M=2 (that is, you will only consider the two previous values in predicting the next one).

(a)

Compute the autocorrelation matrix R. (Assume an extremely long window and don't forget the 1/N normalization).

(b)

Compute the cross correlation vector $\b{g}$.

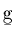(c)

Compute the LPC coefficients.

(d)

Compute the error in prediction.

(e)

Sketch the magnitude response of the all-pole estimator for this signal ( $\hat{\Theta}(z)$).

3.

(From R&S 7.2) Consider an all-pole model of the vocal tract of the form

$$V(z)=\frac{1}{\Pi_{k=1}^q (1-c_kz^{-1})(1-c_k^*z^{-1})}$$

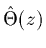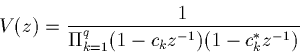
where

$$c_k=r_ke^{j\theta_k}$$

Show that the corresponding cepstrum is

$$\hat{v}(n)=2\sum_{k=1}^q \frac{ (r_k)^n}{n}cos(\theta_kn)$$

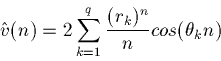
Computer Problems:

4.

Problem 5.23 in DPH. Perform the analysis on utterances of three different vowels. Indicate the expected locations of the first three formants for the vowels you consider.

5.

Using your results from above. Refine your formant estimation procedure for operation on a full sentence. Run the code on the sentence found at:
http://www.cnel.ufl.edu/analog/courses/EEL6586/sentence.html. Discuss your algorithm and show the results on the given sentence.