EEL6586: HW#3

Due Wednesday, March 31, 1999 in class. Late homework will lose $e^{\char93 ~of~days~late} -1$ percentage points. To see the current late penalty, click on
http://www.cnel.ufl.edu/analog/harris/latepoints.html

Noncomputer Problems:

1.

Consider a waveform quantization system with step size d(n), input x(n), and output $\hat x(n)$, where

$$\hat x(n) = \left\{ \begin{array}{ll} 3d(n)/2 & {\rm for~~} ... ...0 \\ -3d(n)/2 & {\rm for~~} x(n) < -d(n) \end{array}\right.$$

$$d(n) = \left\{ \begin{array}{ll} Bd(n-1)+ D & {\rm if~} \ver... ...,n-2, n-3 \\ Bd(n-1)+ E & {\rm otherwise} \end{array}\right.$$

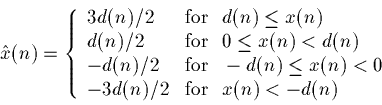
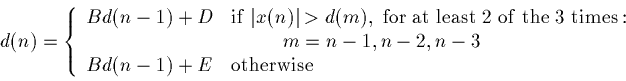
(i.e. D is used if, in two of the last three samples, the input exceeded the step size.). Assume that D>E>0, that d(n)=0 for $n \le 0$, and the the sampling rate of x(n) is 10kHz.

(a)

What is the bit rate if this quantizer codes x(n)?

(b)

Is it necessary to transmit the step size as well as a coded version of 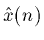$\hat x(n)$ each sample instant? Explain.

(c)

What is the maximum value that d(n) could attain? What sequence of x(n) would lead to such a d(n)? Explain.

(d)

What is the minimum value that d(n) could attain? What sequence of x(n) would lead to such a d(n)? Explain.

(e)

Assume that D=6, E=0, B=0.8 and x(n)=20[u(n-3)-u(n-12)], where u(n) is a step function. Make a table of values of x(n), 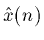$\hat x(n)$, and d(n) for $0 \le n \le 23$.

2.

Derive the recursion for converting the Linear Prediction coefficients to the complex cepstrum (given by equation 6.44 in DPH).

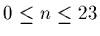Computer Problems:

3.

You will design a simple LPC10-like quantizer for this part. You do not need to find out the exact details of the LPC-10e standard, if fact I would rather that you not. You will demonstrate your coder on the standard sentence at:
http://www.cnel.ufl.edu/analog/courses/EEL6586/sentence.html. Explain your reasoning for each step of the design.

(a)

Perform LPC analysis on the framed sentence. Use which ever order you think is best for minimizing the bitrate while preserving intelligibility.

(b)

Decide voiced vs. unvoiced for each window using any procedure you like. Show a plot showing the voiced vs. unvoiced regions for the sentence.

(c)

If the window is voiced, determine the appropriate pitch period. Show a plot indicating how pitch changes vs. time for this sentence.

(d)

Synthesize the full sentence using only the LPC, pitch, and voiced vs./ unvoiced information. Is the speech intelligible? i.e. would the speech be understood by someone who has never heard the sentence before?

4.

Now you will determine the effect of quantization of your coding parameters.

(a)

Change the number of bits for each LPC coefficient. What is the lowest number of bits where intelligibility is still preserved? What is the corresponding bit rate? (Note: to change the number of bits, find the maximum and minimum values and quantize steps inbetween. This is easiest if you use integers for your representation. Make sure to explain your scheme.)

(b)

Transform the (unquantized) LPC coefficients to a different space. What is the lowest number of bits where intelligibility is still preserved? Synthesize the sentence and write out a a wave file to hand in.

Explain all of your work. As usual, email Kevin matlab code with a wav file with your lowest bit-rate preserving intelligibility. Don't forget to clearly indicate the bit-rate you achieved.