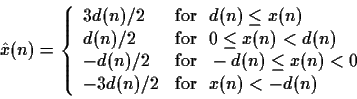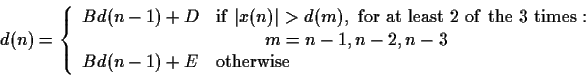Next: EEL6586: HW#4
Up: EEL6586: Homework Assignments
Previous: EEL6586: HW#2
Due Friday, March 23, 2001 in class. Late
homework will lose
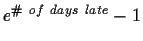 percent.
See
http://www.cnel.ufl.edu/analog/harris/latepoints.html
for penalty.
percent.
See
http://www.cnel.ufl.edu/analog/harris/latepoints.html
for penalty.
PART A: Noncomputer Problems
- A1
- Compute the complex cepstrum of
H(z)=1/(1+.25z-2)
- A2
- Let x1(n) and x2(n) denote two sequences and
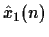 and
and
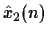 their corresponding complex cepstra. If
their corresponding complex cepstra. If
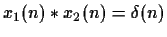 determine the relationship between
determine the relationship between
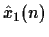 and
and
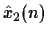 .
.
- A3
- Suppose the complex cepstrum of of y(n) is
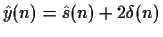 .
Determine y(n) in terms of s(n).
.
Determine y(n) in terms of s(n).
- A4
- Why is the predictor in a DPCM scheme often placed in a feedback loop around the quantizer?
- A5
- Why is a higher-order predictor more often used in DPCM with an
adaptive scheme then in one without time adaptation?
PART B: LPC Hand Analysis of Simplfied Unvoiced Phoneme
Assume that white noise excitation w(n) is filtered by an all-pole
vocal-tract model
H(z)=1/(1+.25z-2)
to produce a speech signal s(n).
w(n) is defined:
In this part, you will use LPC to derive an all-pole approximation
to H(z).
- B1
- Derive the difference equation for s(n). Make sure you get this difference equation correct because you will use it in the next two parts.
- B2
- Compute the autocorrelation function r(0) for the speech signal s(n).
- B3
- Compute the autocorrelation function r(1) and
r(2) for the speech signal s(n).
- B4
- Compute the first two LPC coefficients (p=2).
- B5
- Derive
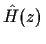 ,
the all-pole approximation to
H(z). Does your answer make sense?
,
the all-pole approximation to
H(z). Does your answer make sense?
PART C: Adaptive Quantization Coder Problem
Consider a waveform quantization system with step size d(n), input
x(n), and output 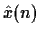 , where
, where
(i.e. D is used if, in two of the last three samples, the input exceeded the
step size.). Assume that D>E>0, that d(n)=0 for 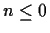 , and the the
sampling rate of x(n) is 10kHz.
, and the the
sampling rate of x(n) is 10kHz.
- C1
- What is the bit rate if this quantizer codes x(n)?
- C2
- Is it necessary to transmit the step size as well as a coded version
of
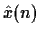 each sample instant? Explain.
each sample instant? Explain.
- C3
- What is the maximum value that d(n) could attain? What sequence of
x(n) would lead to such a d(n)? Explain.
- C4
- What is the minimum value that d(n) could attain? What sequence of
x(n) would lead to such a d(n)? Explain.
- C5
- Assume that D=6, E=0, B=0.8 and
x(n)=20[u(n-3)-u(n-12)], where
u(n) is a step function. Make a table of values of x(n),
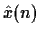 ,
and d(n) for
,
and d(n) for
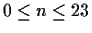 .
.
PART D: Computer Analysis of Speech
You will write two programs for speech analysis. You should run your code
on the two sentences found at:
http://www.cnel.ufl.edu/analog/courses/EEL6586/sentences.html.
- D1
- Write a program that determines the pitch of a signal (F0
in Hz.) We talked about a number of algorithms in class but one of the autocorrelation techniques would be straightforward to implement.
- D2
- Write a program that determines the first three formant
location (F1, F2, F3 in Hz.) We will talk in class about several techniques
but factoring the LPC polynomial is probably the most straightforward.
As always, hand in all of your matlab code. Make sure that your code is your
own, don't download anything from other students or the internet without
proper acknowledgements. Discuss your algorithms in detail and hand in plots
showing the results on the two sentences. Comment on the accuracy of your
algorithms.



Next: EEL6586: HW#4
Up: EEL6586: Homework Assignments
Previous: EEL6586: HW#2
Dr John Harris
2001-04-05
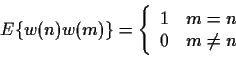
![]() , where
, where