


Next: EEL6586: HW#3
Up: EEL6586: Homework Assignments
Previous: EEL6586: HW#1
Due Monday, February 19, 2001 in class. Late
homework will lose
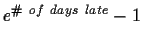 percent.
To see the current late penalty, click
http://www.cnel.ufl.edu/analog/harris/latepoints.html
percent.
To see the current late penalty, click
http://www.cnel.ufl.edu/analog/harris/latepoints.html
PART A: Noncomputer Problems
- A1
- Suppose you are estimating a short-term average magnitude function
using a 200 point Hamming window for a 10KHz sampled speech waveform.
Using Nyquist arguments and some simple assumptions, what is the most you
can reasonably shift the window between applications without losing
information?
- A2
- The short-term energy of a sequence s(n) is defined as
- i
- For the particular choice w(m)=am for
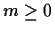 and 0 otherwise,
find a recurrence formula for Q(n) in terms of Q(n-1) and the input
s(n).
and 0 otherwise,
find a recurrence formula for Q(n) in terms of Q(n-1) and the input
s(n).
- ii
- What general property must the window w(m) have in order that it
be possible to find a recursive implementation?
- A3
- Consider the signal
- i
- Find the long-term autocorrelation function r(k) for s(n).
- ii
- Sketch (by hand) r(k) as a function of k. Label important points.
- A4
- A train of impulses is fed through an all-pole model of
H(z)=1/(1+.25z-2). Sketch the time domain waveform for a few
periods assuming fs=3KHz and pitch frequency is 300 Hz. Label all
important parameters. Show all of your hand calculations, you may
check your results with Matlab if you want.
- A5
- Sketch the magnitude of the Fourier Transform for the all-pole signal
created in problem A4. Label all important parameters.
PART B: LPC Example
Consider the infinite-length signal x(n), a short segment is shown below.
Your goal is to derive the LPC coefficients for the prediction of x(n).
Assume order p=2 (that is, you will only consider the two previous values
in predicting the next one).
- B1
- Compute the autocorrelation matrix R (Assume an extremely long
window and include a 1/N normalization factor for parts B1 and B2).
- B2
- Compute cross correlation vector
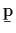 .
.
- B3
- Compute the two LPC coefficients for this problem.
- B4
- What is the resulting error in prediction?
- B5
- Sketch the magnitude response of the all-pole estimator for this
signal (H(z)).
PART C: Computer Analysis of Speech
You will write a program to segment a recorded sentence into three different
components: silence (non-speech), voiced speech and unvoiced speech. You
should run your code on the sentence
found at
http://www.cnel.ufl.edu/analog/courses/EEL6586/sentence.html.
- C1
- Describe (in words) your strategy in writing and improving your
program. A successful labeling program should utilize at least a
short-term energy and a short-term zero crossing measure. However, as
usual, you may add whatever you like to further improve the performance of
your program.
- C2
- Show a plot that, you feel, best depicts the labeling of the test sentence.
- C3
- Have matlab create a table of the starting location of each labelled segment. For instance, you output should look something like the following:
| Sample Number |
Type |
| 1 |
silence |
| 234 |
unvoiced |
| 578 |
voiced |
- C4
- Comment on the accuracy of your algorithm. Make sure to run your code on other sentences to see how generally is can be applied.
- C5
- As always, hand in all of your matlab code.



Next: EEL6586: HW#3
Up: EEL6586: Homework Assignments
Previous: EEL6586: HW#1
Dr John Harris
2001-04-05
![\begin{displaymath}Q(n)=\sum_{m=-\infty}^\infty [s(m)w(n-m)]^2 \end{displaymath}](img4.gif)
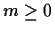 and 0 otherwise,
find a recurrence formula for Q(n) in terms of Q(n-1) and the input
s(n).
and 0 otherwise,
find a recurrence formula for Q(n) in terms of Q(n-1) and the input
s(n).