EEL6502: HW#4

EEL 6502  -  Spring 1998

Due Monday, March 23 by 5pm. As usual, hand in your homework in two distinct parts: hand calculations and final results in part 1 and Matlab code in Part 2.

A1

Problem 5.1 in Clarkson

A2

Problem 5.2 in Clarkson

A3

Problem 5.16 in Clarkson

A4

Consider the adaptive noise cancellation problem where the primary signal is zero-mean Gaussian noise with variance 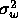(d(n)=w(n)) and the reference signal is equal to one (x(n)=1). Answer the following questions about the LMS implementation of this adaptive filter using a step size parameter 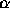. Remember that you only need one tap weight for this problem.

• Using the approximations derived in class (and also in the book), estimate the variance of the the weight value after ``convergence.''
• Compute an exact expression for the variance of the weight.
• Compute an exact expression for the Misadjustment. M.

We have used two microphones to record two channels of a voice signal corrupted by low frequency noise from an electronic alarm clock. The file hw4.mat in the course directory contains two variables d (voice signal plus noise) and x (primarily noise). Download the binary data file in http://www.cnel.ufl.edu/analog/courses/EEL6502/hw4/hw4.mat A few words are spoken with pauses in between. The noise is evident in the pauses between the words. Write an adaptive filter algorithm to reduce the amount of noise in the signal. You can prototype your algorithm on the first few thousand points before running on the entire signal. Draw a block diagram of your system and describe how you chose values for 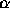and the number of taps in the adaptive filter. As usual, turn in all of your MATLAB code. You only need show plots of:

• The original signal (d) and filtered signal (e). You should see a noticeable reduction of the noise on this plot.
• The original signal and filtered signal zoomed up so that the details of the signals can be seen.
• The values of each of the weights (make sure your weight values have converged).

Feel free to turn in other plots that might be interesting. If you want, you can listen to the signals if your computer supports the MATLAB ``sound'' command. The signals were sampled at 11025Hz.