EEL6502: HW#5

EEL 6502  -  Spring 1998

Due Monday, April 6 by 5pm. As usual, hand in your homework in two distinct parts: hand calculations and final results in part 1 and Matlab code in Part 2.

A1

A student used simple LMS adaptation on an FIR filter to solve a system ID problem with a single sine wave input. She was surprised to find that the output of the adaptive filter had energy at frequency values other than at the original input frequency. How can this be considering the fact that we have said that these filters are linear and therefore cannot create energy at frequencies not present in the original signal? These other frequencies are not due to finite window (or DFT leakage effects).

A2

Consider the system ID problem where 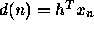, where 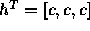(assume c>0) and where x(n) is the 3-periodic sequence 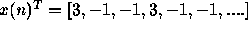Initialize the weights to zero.

• Show that the Sign-Sign algorithm

  

  is always divergent in the sense that ( )

• Find limits on for the conventional LMS algorithm to converge.

B1

6.28 in Clarkson

B2

Consider the system identification problem with an unknown plant having the following very simple system function:

The adaptive filter that is used to model H(z) has two free parameters, a and b, as follows:

The input x(n) to both systems is white Gaussian noise with a variance of one.

1. Express the MSE ( 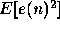) in terms of the free parameters a and b.
2. Using the above result find an expression for the optimal value of a in terms of b.
3. Find numerical values for both a and b.
4. Compute a numerical value for the optimal MSE. Does its value make sense?

C1

6.29 in Clarkson

C2

Once again, consider the adaptive noise cancellation problem where the primary signal is zero-mean Gaussian noise with variance 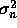(d(n)=w(n)) and the reference signal is equal to one (x(n)=1). Answer the following questions about the exponentially weighted RLS (EWRLS) implementation of this adaptive filter. Remember that you only need one tap weight for this problem.

1. Write an expression for the energy that is minimized by EWRLS at iteration n.
2. Derive an expression for the value of the weight given by EWRLS at iteration n.
3. Compute the variance of the weight at steady-state (i.e. after ``convergence'').
4. What is the variance of the weight for 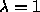and for ? Justify each answer with some words explaining why your values make sense.