EEL6502: HW#3

EEL 6502  -  Spring 1998

Due Friday, February 27 by 5pm. As usual, hand in your homework in two distinct parts. The first part answers all of the questions and contains the numerical results and plots from Matlab with the appropriate descriptions. The second part contains the Matlab code use to generate results in part 1.

Do not use a computer for part A. Consider the following AR sequence:

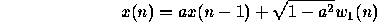
Assume 0<a<1 and that 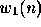is a unity variance, white Gaussian noise signal. This signal is used as input to a system ID problem with a ``unknown filter'' of h(0)=1, h(1)=0. The desired signal d(n) is given by:

A1

Derive expressions for r(0) and r(1). Why did we include the awkward 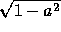term in the generating sequence?

A2

Compute the eigenvectors and eigenvalues of R (for L=2). What is the condition number, k, of R?

A3

What is maximum value of 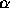that will guarantee stability? Give two sets of answers using equations 4.2.20 and 4.2.23 in Clarkson.

A4

Estimate the convergence rate as a function of a and .

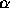Implement the system ID scenario described in part A. Always initialize 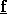to .

B1

Compute r(0) and r(1) for x(n) using Matlab. How do your results compare to A1?

B2

Compute the eigenvectors and eigenvalues of R using Matlab. What is the computed condition number, k, of R? Compare to A2.

B3

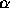What is the highest value of that achieves stability for k=1 and for k=10? Describe how you computed this number in Matlab. Is the highest value of 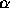a function of k? How do your numbers compare to your analytic calculation given in part A?

B3

What is the convergence rate for k=1 and for k=10? Make sure to turn in properly labeled plots of the J, f(0), f(1) (all vs. iteration number).

B4

Show a 2D plot of 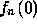vs. 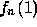for k=1 and for k=10. Explain why the trajectories look the way they do. Hint: for each case sketch contours of constant MSE.

Do not use a computer for part C. Consider the same AR sequence given above in part A but now the desired signal d(n) is corrupted by additional noise as given by:

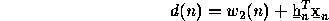
where 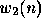is unity variance, white Gaussian noise that is uncorrelated to 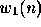. h(n) is the same impulse function as in part A.

C1

What is ?

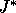C2

What is the steady state mean square error achieved as a function of ?

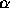C3

What is the variance of the weights upon ``convergence''?

Implement the noisy system ID scenario described in part C.

D1

Are your highest value of 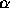any different with the added noise in the desired signal? Explain.

D2

What is the steady state mean square error achieved for several values of 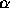? Show plots of J vs. iteration number for different 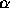values. Compare your results to C2.

D3

What is the variance of the weights upon ``convergence''? Show a few plots of 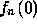vs. iteration for different values of 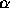. Compare your results to C3.

D4

Show a 2D plot of 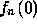vs. 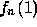for for k=1 and for k=10. Explain why the trajectories look different from those in B4.