


Next: EEL6502: HW#3
Up: EEL6502: Homework Assignments
Previous: EEL6502: HW#1
 EEL 6502 - Spring 1998
EEL 6502 - Spring 1998
Due Monday, February 9 at 5pm. As usual, hand in your homework in two
distinct parts. Part A answers all of the questions and contains the
numerical results and plots from Matlab with the appropriate descriptions.
Part B contains the Matlab code use to generate results in part A.
- A1
- Problem 3.16 Clarkson
- A2
- Problem 3.22 Clarkson
- A3
- You are given the inputs and outputs of an unknown system. You
know that it is FIR but you don't know the order.
The x and d files can be found at
http://www.cnel.ufl.edu/analog/courses/EEL6502/hw2/x.asc
and
http://www.cnel.ufl.edu/analog/courses/EEL6502/hw2/d.asc
Use the Wiener filter formulation we discussed in class to determine the
coefficients of the unknown FIR filter. What are the coefficients?
(This problem is interesting because you don't know order of the system so
some sort of trial and error is expected.)
- A4
- What type of filter is the unknown FIR filter (e.g. high-pass,
band-stop, etc.)? Show a plot of some kind in matlab that justifies your
answer.
A second-order autoregressive (AR) process x(n) is described
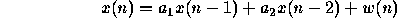
where 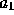 and
and 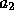 are real-valued constant coefficients, and w(n) is a
white noise process with zero mean and unit variance.
We would like to build a single-step
predicter with a Wiener filter.
Express each of the following in terms of the AR parameters
are real-valued constant coefficients, and w(n) is a
white noise process with zero mean and unit variance.
We would like to build a single-step
predicter with a Wiener filter.
Express each of the following in terms of the AR parameters 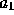 and
and
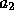 .
.
- B1
- The simplest prediction value is to guess the mean value at each
iteration, i.e. y(n)=0. What is the value of the MSE for this predictor?
- B2
- Another simple estimator is to guess the previous value
i.e. y(n)=x(n). What is the value of the MSE for this predictor?
- B3
- Derive the optimal Wiener Filter weights f(0) and f(1). Show
all of your work. What is the MSE for the Wiener Filter?
Can the MSE computed above be reduced by adding more taps? Explain.
- B4
- Problem 3.20
Do the following parts using Matlab (or similar program).
- C1
-
Let
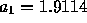 and
and 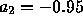 for the second order AR sequence.
Implement the three predictors
discussed in B1, B2, and B3 in Matlab. What are the three prediction errors
(
for the second order AR sequence.
Implement the three predictors
discussed in B1, B2, and B3 in Matlab. What are the three prediction errors
( 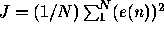 ) and how do they compare to your estimates in B?
) and how do they compare to your estimates in B?
- C2
- Download the data file in
http://www.cnel.ufl.edu/analog/courses/EEL6502/hw2/sunspots.asc This file
contains the number of sunspots observed for each month between 1947 and
1991. Run your wiener filter for single-step prediction for a length L=10.
What is the prediction error over the whole sequence. (you have to discard
the first L of the data samples when you compute the error)
- C3
-
How does your prediction error change with the size of the Wiener filter?
Does your Wiener filter always perform better than the estimators described
in B1 and B2?
- C4
- Is the sunspot sequence an ARMA series?



Next: EEL6502: HW#3
Up: EEL6502: Homework Assignments
Previous: EEL6502: HW#1
Dr John Harris
Thu Apr 2 18:21:08 EST 1998
![]() EEL 6502 - Spring 1998
EEL 6502 - Spring 1998
![]()
![]() and
and ![]() are real-valued constant coefficients, and w(n) is a
white noise process with zero mean and unit variance.
We would like to build a single-step
predicter with a Wiener filter.
Express each of the following in terms of the AR parameters
are real-valued constant coefficients, and w(n) is a
white noise process with zero mean and unit variance.
We would like to build a single-step
predicter with a Wiener filter.
Express each of the following in terms of the AR parameters ![]() and
and
![]() .
.