


Next: EEL6825: HW#2
Up: EEL6825: Homework Assignments
Previous: EEL6825: Homework Assignments
Get PDF file
Due Friday, September 7, 2001 in class. Late homework will
lose
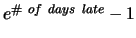 percentage points. Click on
http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
to see the current penalty. A computer is not necessary for this
assignment.
percentage points. Click on
http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
to see the current penalty. A computer is not necessary for this
assignment.
- You are given the following two 1-D distributions which are valid
for all values of x:
Assume that
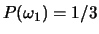 and
and
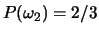
- Compute the posterior probability
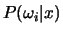 for each
class.
for each
class.
- Derive the Bayes classifier for this problem. In other words, how
would you classify new data points
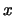 ?
?
- Sketch a plot that graphically indicates the Bayes error.
- Compute the numerical value of the Bayes error for this problem.
- Compute the value of the Bhatacharrya bound for this problem.
Remember that these are not normal distributions.
- Three one-dimensional distributions are given as uniform in [0,1]
for
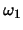 , uniform in [0,2] for
, uniform in [0,2] for 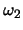 and uniform in
[0,3] for
and uniform in
[0,3] for 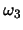 . Assume the a priori probabilities are
equal.
. Assume the a priori probabilities are
equal.
- Compute
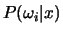 for each class and sketch each function on a
separate plot.
for each class and sketch each function on a
separate plot.
- Describe the Bayes classifier for the three distributions. Be sure to
describe the class for each possible value of
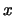 .
.
- Compute the Bayes error for this problem.
- Two normal distributions are characterized by:
Derive the analytic form and sketch the Bayes decision boundary for the following cases:
(Also sketch some equi-probability
contours for each distribution.)
-
-
-
- Problem 2-6 in DH&S
- Problem 2-13 in DH&S
- (Extra credit) 2-32 in DH&S



Next: EEL6825: HW#2
Up: EEL6825: Homework Assignments
Previous: EEL6825: Homework Assignments
Dr John Harris
2001-11-26
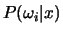 for each
class.
for each
class.
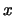 ?
?
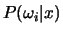 for each class and sketch each function on a
separate plot.
for each class and sketch each function on a
separate plot.
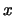 .
.
![\begin{displaymath}\mu_1=
\left[
\begin{array}{c}
0 \\
1
\end{array}
\rig...
...2=
\left[
\begin{array}{c}
0 \\
-1
\end{array}
\right]
\end{displaymath}](img12.gif)
![\begin{displaymath}\Sigma_2=
\left[
\begin{array}{cc}
2&0 \\
0&1
\end{array}
\right]
\end{displaymath}](img15.gif)
![\begin{displaymath}\Sigma_1=
\left[
\begin{array}{cc}
1&.5 \\
.5&1
\end{array}
\right]
\end{displaymath}](img16.gif)
![\begin{displaymath}\Sigma_2=
\left[
\begin{array}{cc}
1&-0.5 \\
-0.5&1
\end{array}
\right]
\end{displaymath}](img17.gif)