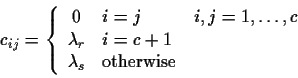Next: EEL6825: HW#2
Up: EEL6825: Homework Assignments
Previous: EEL6825: Homework Assignments
Due Friday, Friday, September 10, 1999 in class. Late
homework will lose
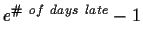 percentage points.
To see the current late penalty, click on
percentage points.
To see the current late penalty, click on
http://www.cnel.ufl.edu/analog/harris/latepoints.html
A computer is not necessary for this assignment.
- 1.
- Three one-dimensional distributions are given as uniform in [-1/3,1/3] for
 ,
uniform in [-1/2,1/2] for
,
uniform in [-1/2,1/2] for  and uniform in [-1,1] for
and uniform in [-1,1] for
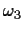 .
Assume the a priori probabilities are equal.
.
Assume the a priori probabilities are equal.
- (a)
- Compute
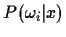 for each class and sketch each function on a
separate plot.
for each class and sketch each function on a
separate plot.
- (b)
- Implement a Bayes classifier for the three distributions. Be sure to
describe the class for each possible value of x.
- (c)
- Compute the Bayes error.
- 2.
- Two normal distributions are characterized by:
Derive the analytic form and sketch the Bayes decision boundary for the following cases:
(Also sketch some equi-probability
contours for each distribution.)
- (a)
-
- (b)
-
- (c)
-
- 3.
- In many pattern classification problems one has the option either to
assign the pattern to one of c classes or to reject it as being
unrecognizable. If the costs for rejects is not too high, rejection may be a
desirable action. Let
where 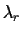 is the loss incurred for choosing the (c+1)th action of
rejection, and
is the loss incurred for choosing the (c+1)th action of
rejection, and 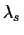 is the loss incurred for making a substitution
error. Show that the minimum risk is obtainable if we decide
is the loss incurred for making a substitution
error. Show that the minimum risk is obtainable if we decide 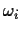 if
if
 for all j and if
for all j and if
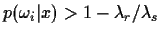 and reject otherwise. What
happens if
and reject otherwise. What
happens if
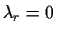 ? What happens if
? What happens if
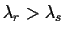 ?
?
- 4.
- Problem 2.6 in T&K (Neyman-Pearson Test)
- 5.
- Problem 2.9 in T&K (Analytic form of Bayes error for normal distributions)



Next: EEL6825: HW#2
Up: EEL6825: Homework Assignments
Previous: EEL6825: Homework Assignments
Dr John Harris
1999-12-10
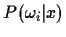 for each class and sketch each function on a
separate plot.
for each class and sketch each function on a
separate plot.
![\begin{displaymath}\mu_1=
\left[
\begin{array}{c}
0 \\
1
\end{array}\right]
,
\mu_2=
\left[
\begin{array}{c}
0 \\
-1
\end{array}\right]
\end{displaymath}](img8.gif)
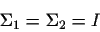
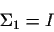
![\begin{displaymath}\Sigma_2=
\left[
\begin{array}{cc}
2&0 \\
0&1
\end{array}\right]
\end{displaymath}](img11.gif)
![\begin{displaymath}\Sigma_1=
\left[
\begin{array}{cc}
1&.5 \\
.5&1
\end{array}\right]
\end{displaymath}](img12.gif)
![\begin{displaymath}\Sigma_2=
\left[
\begin{array}{cc}
1&-0.5 \\
-0.5&1
\end{array}\right]
\end{displaymath}](img13.gif)