EEL6825: HW#2

Due Friday, Friday, Sept. 24, 1999 in class. Late homework will lose 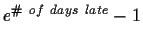$e^{\char93 ~of~days~late} -1$ percentage points. To see the current late penalty, click on
http://www.cnel.ufl.edu/analog/harris/latepoints.html

PART A: Textbook Problems Answer the following questions, you should not use a computer.

A1

It is well known that if two normal distributions have the same covariance matrix, the Bayes discrimination function is linear. However, given two non-normal probability distributions are identical, except for their means, is the Bayes classifier necessarily linear? Why or why not?

A2

Sample data from one class are given as:

$$\left[ \begin{array}{c} 0 \\ 0 \end{array} \right] \left[ \be... ...} \right] \left[ \begin{array}{c} -1 \\ -1 \end{array} \right]$$

Compute the sampled mean and sampled covariance matrix. Make sure to use estimators that are unbiased. Show your work.

A3

You are given the heights and weights of a certain set of individuals in unknown units. Which one of the following six matrices is the most likely to be the sampled covariance matrix? Explain your reasoning.

      1.232 0.013      1.232 0.867     1.232 -0.867 
      0.013 2.791     -0.867 2.791    -0.867  3.307


      1.232 3.307      1.232 0.867     1.232  3.307
      0.013 2.791      0.867 2.791     3.307  2.791

A4

2.20 in T+K

A5

3.2 in D+H

PART B: Computer Experiment: Bayes Classifier with two classes and synthetic data Two normal distributions are characterized by:

$$P(\omega_1)=P(\omega_2)=0.5$$

$$\mu_1= \left[ \begin{array}{c} 0 \\ 0 \end{array}\right] , \... ...= \left[ \begin{array}{cc} 1&0.9 \\ 0.9&1 \end{array}\right]$$

B1

Generate 100 points from each of these distributions. Show a scatter plot of the data using two different symbols to identify the classes.

B2

Compute the sampled mean and covariance matrix for each class. How close are these values to the true mean and covariance matrix?

B3

Write a matlab program that classifies the data using a Bayes Classifier. Assume the data comes from Normal distributions but use your estimated parameters in the classifier. What is the percent error that you find? Run your program several times and average your results to improve your estimate of the expected error.

B4

Compute the Bhatacharrya bound for this problem can compare to your actual error from [B3]. Remember from class that the Bhatacharrya bound is an upper bound on the Bayes error for Normal distributions and is given by:

$$BOUND= e^{-K}\sqrt{P(\omega_1) P(\omega_2)}$$

where K is given by:

$$K=\frac{1}{8}(\mu_2-\mu_1)^T[\frac{\Sigma_1+\Sigma_2}{2}]^{-1... ...igma_2}{2}\vert}{\sqrt{\vert\Sigma_1\vert\vert\Sigma_2\vert}})$$

This equation can be found on page 99 of Fukanaga's textbook if you want to read more about it. However all of the information you need is provided above. Again use the estimated parameters in your calculation.

B5

Have the computer draw the decision surface on the scatter plot. (Do not hard code the particular boundary for this problem, you should write a general program.) Hint: think about using the functions meshgrid and contour in matlab.

PART C: Computer Experiment with Bayes Classifier with 3 classes and real data

You are given the heights and weights of all of the players in the NBA (National Basketball Association) at the end of last season. The file can be found in
http://www.cnel.ufl.edu/analog/courses/EEL6825/nba.asc Each line of the file consists of four numbers: (1) Player's position. 1=guard 2=forward 3=center. (Guards are usually smaller than forwards who are usually smaller than centers.) (2) Player's height: truncated value in feet (3) Player's height - truncated value: in inches (4) Player's weight: pounds.

C1

Read in the data and print a scatter plot showing the three different classes with height on the x₁ axis and weight on the x₂axis. Are any two of the classes linearly separable?

C2

Compute the sampled mean and covariance matrix for each position.

C3

Assume that all three classes are generated from normal distributions. Also assume that the a priori probabilities are set by the number of points in each class. Design a Bayes classifier using the sampled mean and covariance matrix. What is the percent classification error?

C4

Using a similar technique as [B5], draw the discriminant boundaries on the scatter plots.

C5

What position would you play if you played in the NBA? What position would you play if you were exactly one foot taller?

Final note:

Your homework should be in two distinct parts. The first part should show the answers, plots, hand calculations etc. that you need to answer the questions. The second part should contain all of the Matlab code that you have written to generate the answers in the first part.