


Next: EEL6825: HW#3
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#1
Due Friday, September 25, 1998 in class. Do not be late to class. Late
homework will lose
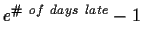 percentage points. Do not hand
in any matlab code or plots-instructions for turning in matlab code will be
discussed in class.
percentage points. Do not hand
in any matlab code or plots-instructions for turning in matlab code will be
discussed in class.
PART A: Textbook Problems
- A1
- 3.1 in DH&S
- A2
- 3.2 in DH&S
- A3
- 3.6 in DH&S
- A4
- 3.7 in DH&S
- A5
- 5.4 in DH&S
PART B: Short-Answer Problems
Answer each of the following with a short statement, derivation
and/or sketch.
- B1
- If x is a 1D random variable given by a normal distribution with
mean
 and variance
and variance 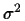 ,
what is
,
what is 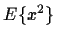 ?
?
- B2
- It is well known that if two normal distributions have the same
covariance matrix, the Bayes discrimination function is linear. However,
given two non-normal probability distributions are identical, except
for their means, is the Bayes classifier necessarily linear? Why or why
not?
- B3
- You are given data drawn from two Normal distributions. It
turns out that the data points are linearly separable. Is the Bayes
Classifier you design guaranteed to correctly classify all of the data
points?
- B4
- A certain classifier
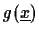 gives an error of 55% on
a given dataset for a two-category classification problem. Explain a
simple way of improving the performance of this classifier on the same
data.
gives an error of 55% on
a given dataset for a two-category classification problem. Explain a
simple way of improving the performance of this classifier on the same
data.
- B5
- Write an equation for a linear classifier that successfully
classifies points (1,1) and (2,0) as class
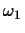 and points
(2,1) and (3,0) as class
and points
(2,1) and (3,0) as class 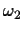 .
.
turn over
PART C: Computer Experiment: Bayes Classifier with 3 classes
You are given the heights and weights of all of the players in the WNBA
(Women's National Basketball Association) at the end of last season.
The file can be found in
http://www.cnel.ufl.edu/analog/courses/EEL6825/wnba.asc
Each line of the file consists of four numbers:
(1)
Player's position. 1=guard 2=forward 3=center. (Guards are usually
smaller than forwards who are usually smaller than centers.) (2)
Player's height: truncated value in feet
(3) Player's height - truncated value: in inches
(4) Player's weight: pounds.
- C1
- Read in the data and print a scatter plot showing the three
different classes with height on the x1 axis and weight on the x2axis. Are any two of the classes linearly separable?
- C2
- Compute the sampled mean and covariance matrix for each position.
- C3
- Assume that all three classes are generated from normal
distributions with equal a priori probabilities.
Design a Bayes classifier using the sampled mean and covariance
matrix.
Draw the discriminant boundaries on the scatter plots.
How many players are classified incorrectly?
- C4
- Can you draw two linear boundaries by hand
that classify better than
the sampled Bayes Classifier?
- C5
- What position would you play
if you played in the WNBA?



Next: EEL6825: HW#3
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#1
Dr John Harris
1998-12-19