


Next: EEL6825: HW#2
Up: EEL6825: Homework Assignments
Previous: EEL6825: Homework Assignments
Due Friday, September 11, 1998 in class. Do not be late to class. Do not
hand in any matlab code or plots-instructions for turning in matlab code
will be discussed in class.
- 1.
- Three one-dimensional distributions are given as uniform in [-1/3,1/3] for
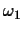 ,
uniform in [-1/2,1/2] for
,
uniform in [-1/2,1/2] for 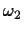 and uniform in [-1,1] for
and uniform in [-1,1] for
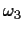 .
.
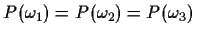 .
.
- (a)
- Compute
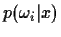 for each class and sketch each function on a
separate plot.
for each class and sketch each function on a
separate plot.
- (b)
- Consider a Bayes classifier for the three distributions. Be sure to
describe the class for each possible value of x.
- 2.
- 2.5 in DH&S
- 3.
- 2.6 in DH&S
- 4.
- 2.10 in DH&S
- 5.
- Two normal distributions are characterized by:
- (a)
- Plot the contours of constant d2(X)
(constant Mahalanobis distance) for each distribution by setting d2(X)=1for each contour. Clearly label each contour.
- (b)
- Compute the Bayes classifier (g(x)).
- (c)
- Sketch the Bayes Classifier on a graph
that also shows probability contours. Clearly label the classification
regions.
- 6.
- Computer Exercise 2.7 in DH&S



Next: EEL6825: HW#2
Up: EEL6825: Homework Assignments
Previous: EEL6825: Homework Assignments
Dr John Harris
1998-12-19
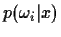 for each class and sketch each function on a
separate plot.
for each class and sketch each function on a
separate plot.
![\begin{displaymath}\mu_1=\mu_2=
\left[
\begin{array}{c}
0 \\
0
\end{array}\right]
\end{displaymath}](img8.gif)
![\begin{displaymath}\Sigma_1=
\left[
\begin{array}{cc}
1&0 \\
0&1/4
\end{array}\right]
\end{displaymath}](img9.gif)
![\begin{displaymath}\Sigma_2=
\left[
\begin{array}{cc}
1/4&0 \\
0&1
\end{array}\right]
\end{displaymath}](img10.gif)