


Next: About this document ...
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#4
Due Wednesday, December 4, 1998 in class. Do not be late to class. Late
homework will lose
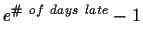 percentage points.
Click on
percentage points.
Click on
http://www.cnel.ufl.edu/analog/harris/latepoints.html
to see the penalty. Also, if you are presenting your project that day, your
homework is due on Dec. 7, 1998.
PART A: Short Questions
- A1
- Suppose a student is given data that consists of many 2-D samples of the 1-D
curve described by:
x12+x22=1 where 0>x1>1. Why can't the
standard K-L transform accurately represent this data in one dimension?
Sketch the likely result of using the K-L transform to reduce the dimension
for this problem.
- A2
- The density function of a two-dimensional random vector x consists of four
impulses at (0,3) (0,1) (1,0) and (3,0) with probability of 1/4 for each.
Find the K-L expansion. Compute the mean-square error when one feature is
eliminate. Compute the contribution of each point to the mean-square error.
PART B: Continuous Distribution
You are given two three-dimensional normal
distributions with the following means and
covariance matrices:
![$\mu_1=
\left[
\begin{array}{c}
-1 \\
1 \\
0
\end{array}\right]
$](img22.gif)
![$\mu_2=
\left[
\begin{array}{c}
1 \\
-1 \\
0
\end{array}\right]
$](img23.gif)
![$\Sigma_1=
\left[
\begin{array}{ccc}
1&0&0 \\
0&1&0 \\
0&0&0
\end{array}\right]
$](img24.gif)
![$\Sigma_2=
\left[
\begin{array}{ccc}
5&2&0 \\
2&1&0 \\
0&0&0
\end{array}\right]
$](img25.gif)
Assume that
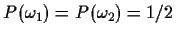 Answer the following questions
relating to using the K-L transform for dimensionality reduction.
Answer the following questions
relating to using the K-L transform for dimensionality reduction.
- B1
- Compute the combined mean (
 )
and covariance matrix (
)
and covariance matrix (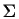 )
for the
data in this problem.
Hint: Remember that the combined distribution of two equally likely
normal distributions
is not a normal distribution but the combined covariance matrix
can be expressed as:
)
for the
data in this problem.
Hint: Remember that the combined distribution of two equally likely
normal distributions
is not a normal distribution but the combined covariance matrix
can be expressed as:
- B2
- Compute all of the eigenvalues and eigenvectors of
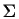 .
.
- B3
- If you had to drop one linear feature, which eigenvalue direction would you
drop? Comment on the likely resulting change (if any) in the error for
representation and for classification.
- B4
- If you had to drop two linear features, which
two eigenvalue directions would you
drop? Comment on the likely resulting change (if any) in the error for
representation and for classification.
- B5
- Draw a very rough sketch 2-D sketch of the two distributions and show the
key linear features under consideration. You do not have to draw exact
equiprobability contours for each distribution. Make clear which direction
you are deciding to keep (from your answer to part B4).
PART C: Computer Experiments
- C1
- Reduce the dimensionality of the sonar data (from HW#3) using the
K-L Transform. Obviously, you must use exactly the same linear transform
on both classes. Build a nearest neighbor classifier in this reduced
dimension space. How does the resulting 1-NN leave-one-out error change
with dimensionality? Explain your observations.
- C2
- Extra credit (10 points). Make up a two-dimensional two-class
classification problem with the following characteristic: a neural network
with 3 hidden units should perform significantly better than one with 2
hidden units. Hint: choose as few points as possible so that your program
will run fast. Try the neural network code from your last assignment on
this problem and report the errors and show the classification boundaries
for networks with 2 and 3 hidden units.



Next: About this document ...
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#4
Dr John Harris
1998-12-19
![$\mu_1=
\left[
\begin{array}{c}
-1 \\
1 \\
0
\end{array}\right]
$](img22.gif)
![$\mu_2=
\left[
\begin{array}{c}
1 \\
-1 \\
0
\end{array}\right]
$](img23.gif)
![$\Sigma_1=
\left[
\begin{array}{ccc}
1&0&0 \\
0&1&0 \\
0&0&0
\end{array}\right]
$](img24.gif)
![$\Sigma_2=
\left[
\begin{array}{ccc}
5&2&0 \\
2&1&0 \\
0&0&0
\end{array}\right]
$](img25.gif)
![$\mu_1=
\left[
\begin{array}{c}
-1 \\
1 \\
0
\end{array}\right]
$](img22.gif)
![$\mu_2=
\left[
\begin{array}{c}
1 \\
-1 \\
0
\end{array}\right]
$](img23.gif)
![$\Sigma_1=
\left[
\begin{array}{ccc}
1&0&0 \\
0&1&0 \\
0&0&0
\end{array}\right]
$](img24.gif)
![$\Sigma_2=
\left[
\begin{array}{ccc}
5&2&0 \\
2&1&0 \\
0&0&0
\end{array}\right]
$](img25.gif)
![]() Answer the following questions
relating to using the K-L transform for dimensionality reduction.
Answer the following questions
relating to using the K-L transform for dimensionality reduction.