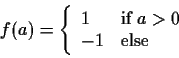EEL6825: HW#4

Due Wednesday, November 4, 1998 in class. Do not be late to class. Late homework will lose $e^{\char93 ~of~days~late} -1$ percentage points.
Click on (http://www.cnel.ufl.edu/analog/harris/latepoints.html). Also, I will not look at any part of your assignment on the computer. Please hand in a hardcopy of all plots and all of your Matlab code. You must write code of some sort-you cannot use a neural network simulator for this problem.

PART A: Textbook Problems

A1

6.1 in DH&S

A2

Compare and contrast nearest-neighbor classification with neural networks in terms of computation time required for (a) training and (b) classification.

A3

You are given two two-dimensional data distributions. All Class 1 points fall inside the square defined by 0<x₁<1 and 0<x₂<1. All Class 2 points fall outside this square. Assume the sigmoid activation function of the neural network to be:

$$f(a) = \left\{ \begin{array}{ll} 1 & \mbox{if $a>0$} \\ -1 & \mbox{else} \end{array} \right.$$

(a)

Draw the simplest neural network configuration that can correctly classify all of the data points. The final output of your neural network should be +1 for class 1 and -1 for class 2.

(b)

Do you need a hidden layer for this problem? Explain. If you require a hidden layer, provide all the weight values for the hidden layer. Explain your reasoning.

(c)

Compute all the remaining weight values (e.g. output layer). The final output of your neural network should be +1 for class 1 and -1 for class 2. Explain your reasoning.

A4

In problem A3, we used a neural-network with a step function instead of the usual sigmoid function. What is the major problem with using the step function in solving practical pattern recognition problems?

A5

Consider a simple example of a network involving a single weight for which the cost function is

E(w)=k₁(w-w_o)² + k₂

where w_o, k₁, and k₂ are constants. A backpropagation algorithm with momentum is used to minimize E(w). How does the momentum constant 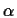$\alpha$ change the convergence rate for this system? Explain.

PART B: Computer Experiment: Neural Networks

This part of the homework concerns two-class classification of a two-dimensional dataset. Load the data from the files http://www.cnel.ufl.edu/analog/courses/EEL6825/x1.asc and http://www.cnel.ufl.edu/analog/courses/EEL6825/x2.asc The x1 and x2 arrays contain the list of two-dimensional points in each class.

Note: Goose has provided a single file that consists a randomized list of points with an additional binary label specifying membership in class 2. Look at http://www.cnel.ufl.edu/analog/courses/EEL6825/x1x2.asc

B1

Write a program that performs gradient descent for a linear perceptron (MLP with no hidden units) and a single output node. Describe your strategy and hand in your code.

B2

Run the linear perceptron program for the provided data set. Plot the boundary your program obtains and give the resulting error.

B3

Develop a single output, single hidden-layer perceptron algorithm that can classify the data set. Explain your strategy in programming.

B4

Plot the decision boundary used by the neural network for a good choice of hidden nodes. What is the resulting error?

B5

How does the error for the MLP change with the number of hidden units? Do your results make sense?