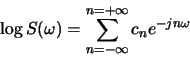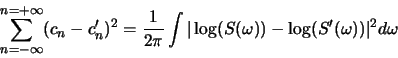Next: EEL6586: HW#4
Up: EEL6586: Homework
Previous: EEL6586: HW#2
Get PDF file
EEL 6586: HW#3
Assignment is due Friday, February 22, 2008 in class. Late
homework loses
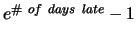 percentage
points.
PART A: Short Answer (No more than a few sentences each)
percentage
points.
PART A: Short Answer (No more than a few sentences each)
- A1
- Assume that a speech signal was framed with a 25ms rectangular window. What is the main lobe width in
Hz due to the rectangular window? Recall that the main lobe width appears in the Fourier magnitude spectrum of
speech as the width of each pitch harmonic. Assume a 20KHz sampling rate.
- A2
- A common algorithm for pitch determination is to
perform
autocorrelation on the LPC residual (error) and look for peaks. Why does
this algorithm work better than performing autocorrelation on the original
speech signal and looking for peaks?
- A3
- The following synthetic sound is created:
What is the likely pitch frequency we would perceive in listening to this sound? Explain.
- A4
- Compute the complex cepstrum of
Assume 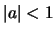 .
.
- A5
- In class, the cepstrum was defined as the inverse Fourier Transform of the log of the Fourier Transform. However, some people define the cepstrum
as the Fourier Transform of the log of the Fourier Transform (without the inverse). Which version do you expect to perform better in actual applications?
Explain.
PART B: Textbook problems (Use Matlab only to optionally check your work)
- B1
- Derive an exact value for the height of the first side band of the rectangular window.
Make whatever assumptions you feel necessary.
- B2
- Compute the real cepstrum of
Assume 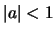 .
.
- B3
- Compute the complex cepstrum of the following causal filter
- B4
- The cepstral coefficients of a recorded speech signal
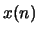 are given by
are given by 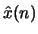 . How do these cepstral
coefficients change when a pre-emphasis factor of
. How do these cepstral
coefficients change when a pre-emphasis factor of  is applied to the speech creating a modified signal
is applied to the speech creating a modified signal
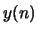 ? Write an equation for
? Write an equation for 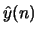 .
.
- B5
- Euclidean distance in complex cepstral space can be
related to a RMS log spectral distance measure. Assuming that
where 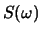 is the power spectrum (magnitude-squared Fourier
transform), prove the following:
is the power spectrum (magnitude-squared Fourier
transform), prove the following:
where 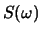 and
and 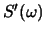 are the power spectra for two
different signals.
are the power spectra for two
different signals.
PART C: Computer Analysis of Speech
In this part you will write a program for automatic pitch analysis.
You will run your program on three recorded sentences at
http://www.cnel.ufl.edu/hybrid/courses/EEL6586/sentence.html
for an adult male (sentence 1), adult female (sentence 2) and a child (sentence 3).
Through the following steps, you will develop a pitch
algorithm that processes the autocorrelation of the LPC residue for
each window of speech:
- C1
- Break the sentence into overlapping windows. Describe how you selected the window type, length and
overlap for this pitch estimation algorithm.
- C2
- Compute the LPC coefficients for each window and inverse filter the signal in that window to get the residue.
Show a typical example of the windowed signal, with plots of the time domain signal, its power spectrum, the smooth
envelope from the LPC coefficients, and the residue (in the time domain).
- C3
- Run an autocorrelation on the residue signal and show an example plot using the residue from [C2].
- C4
- Write a procedure that automatically computes the pitch by finding the ``first biggest peak" after the lag
zero peak. What pitch is detected for your example window from [C3]?
- C5
- Put all of the pieces together and write an algorithm to compute pitch for each window
Write a program that determines the pitch in each window of a sentence (if the pitch exists). Show a plot of F0 (in
Hz) vs. time (in seconds). You may need to add an additional filtering step to smooth out the pitch values.
Indicate unvoiced regions and silence with a pitch of zero.
Hand in plots showing the results on the three sentences. Compute the average pitch of each sentence making sure
to only consider the voiced regions.
As always, hand in all of your Matlab code as
the appendix of your homework. Discuss your algorithms in detail and comment on the accuracy of your algorithms.



Next: EEL6586: HW#4
Up: EEL6586: Homework
Previous: EEL6586: HW#2
Dr John Harris
2008-03-19