


Next: EEL6586: HW#3
Up: EEL6586: Homework
Previous: EEL6586: HW#1
Get PDF file
EEL 6586: HW#2
Assignment is due Friday, January 30, 2004 in class. Late
homework loses
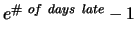 percentage
points. See the current late penalty at http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
You must hand in your homework AND email your two
audio files as attachments to to the TA (Lingyun Gu, lygu@cnel.ufl.edu) by the due date/time. Name your files with your first initial and lastname with -b for
part b and -c for part c. So for example, your professor's files would be called jharris-b.wav and jharris-c.wav
Use a subject
line of ``EEL6586 HW#2 your full name", so for example the professor's subject line would
be ``EEL6586 HW#1 John Harris" You writeup should contain an appendix that includes all of the
matlab code that you wrote for this assignment. You do not need
to include any of the code in Parts A, B, or C but you should
describe your solution technique in these parts.
PART A: Glottal Modelling (Adapted from the Quatieri text)
Consider the following two-pole model for the glottal pulse:
percentage
points. See the current late penalty at http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
You must hand in your homework AND email your two
audio files as attachments to to the TA (Lingyun Gu, lygu@cnel.ufl.edu) by the due date/time. Name your files with your first initial and lastname with -b for
part b and -c for part c. So for example, your professor's files would be called jharris-b.wav and jharris-c.wav
Use a subject
line of ``EEL6586 HW#2 your full name", so for example the professor's subject line would
be ``EEL6586 HW#1 John Harris" You writeup should contain an appendix that includes all of the
matlab code that you wrote for this assignment. You do not need
to include any of the code in Parts A, B, or C but you should
describe your solution technique in these parts.
PART A: Glottal Modelling (Adapted from the Quatieri text)
Consider the following two-pole model for the glottal pulse:
with 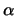 and
and  both real, positive, and less than one,
and where the region of convergence includes the unit circle.
both real, positive, and less than one,
and where the region of convergence includes the unit circle.
- A1
- Derive the inverse z-transform of
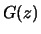 . Show that
. Show that
![$g[n]$](img14.gif) can be expressed as the convolution of two decaying
exponentials.
can be expressed as the convolution of two decaying
exponentials.
- A2
- Use matlab to plot
![$g[n]$](img14.gif) and
and 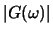 .
Assume
.
Assume 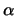 and
and  are close to unity, say, about 0.95.
Why is
are close to unity, say, about 0.95.
Why is 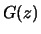 a reasonable model for the spectral magnitude but
a reasonable model for the spectral magnitude but ![$g[n]$](img14.gif) is not a good model glottal shape pulse?
is not a good model glottal shape pulse?
- A3
- Explain why an improved model for the glottal pulse is given by
Derive the z-transform of ![$ \tilde{g}[n] $](img17.gif) . Where are the poles of
. Where are the poles of ![$ \tilde{g}[n] $](img17.gif) in relation to those of
in relation to those of ![$g[n]$](img14.gif) ?
?
- A4
- Consider the periodic glottal waveform
where P is the pitch period and ``*'' denotes convolution.
Plot the Fourier transform magnitude of the windowed glottal flow waveform ![$x[n]$](img19.gif) for a rectangular window with length equal to P and also 2P.
for a rectangular window with length equal to P and also 2P.
- A5
- Which window length would be used in the
calculation of a narrowband spectrogram of the glottal flow waveform? Why? Plot an example narrowband spectrogram.
PART B: Recording a voiced phoneme
- B1
- Record yourself on a computer saying the phoneme /i/
for about 0.5 seconds. Remember the /i/ is the vowel sound in ``me''. Make sure to hold the microphone to the side
of your mouth to reduce noise from the airflow. Email in the sound file as described above as an 8KHz .wav file.
If you have no capability to record sound on a PC and have no friends who can help, talk to the
TA. The recording must be your voice.
- B2
- Hand in a portion of the time domain plots for the phoneme
showing a few pitch periods. The axes of this plot (and all plots)
should be clearly labelled. Clearly indicate the pitch period and
note its numerical value. Also, list the pitch frequency. Is your pitch within its expected range?
- B3
- Plot the magnitude spectrum of the phoneme. Clearly
indicate the values of F
 , F
, F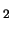 and F
and F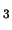 on the graphs. Also show the log magnitude plot.
on the graphs. Also show the log magnitude plot.
- B4
- Estimate the bandwidth and amplitude of each formant using whichever
definition you like. However, be sure to explain your calculation.
- B5
- Plot the spectrogram of the vowel. Show results from
using both short and long windowing functions. Explain what features you can see
each version of the spectrogram that you cannot see in the other.
PART C: Formant Synthesis of a Voiced Vowel
In this part you will try to match your recorded phoneme using formant synthesis. Make sure that you
properly answer all of the questions and describe your solution
technique for each part. You may talk to other students, in
fact you are strongly encouraged to do so. However, the final work
and matlab code you turn in MUST be your own. Some components of this
part are open-ended where there are many possible solution
methods.
- C1
- Write a matlab program that can filter a signal using
the
sum of the output of three bandpass filters. Each bandpass filter will be
specified by a center frequency, a bandwidth and an amplitude. Draw a block diagram of your computation. This is an
open-ended question, use your best judgment in the filter design
but explain your reasoning. Hint: if your formants are too narrow then your phoneme will sound like a musical tone.
- C2
- Use the code in [C1] to filter a train of impulses of
appropriate pitch to
mimic the recorded phoneme from part B. Use the pitch period you derived in part [B2]. In one sentence, describe
how the synthetic sound sounds.
- C3
- Filter an impulse train of more realistically shaped
pulses-assume a duty
cycle of about 50%. For instance, you can use the model from part A. Feel free to tweak other parameters and add anything to the algorithm in order
to improve the quality of the sound.
Hand in a 1/2 second
sound file (8KHz .wav file) of your best synthetic sound. Make sure you describe exactly what you have done to
create this sound. Bonus points will be given to the highest quality, most realistic synthetic sound(s) in the class.
- C4
- Plot time and frequency domain representations of the
vowel (don't use spectrograms). Compare your synthetic sound
results to the recorded sound. In what ways do they differ, if any?
- C5
- Listen to the real and synthetic sounds. In what ways
do they sound
different?



Next: EEL6586: HW#3
Up: EEL6586: Homework
Previous: EEL6586: HW#1
Dr John Harris
2004-04-02
![\begin{displaymath}x[n]=\tilde{g}[n]*\sum_{k=-\infty}^{+\infty} \delta[n-kP]\end{displaymath}](img18.gif)