EEL6586: HW#1

Get PDF file

EEL 6586: HW#1

Assignment is due Friday, January 16, 2004 in class. Late homework loses $e^{\char93  of days late} -1$ percentage points. See the current late penalty at http://www.cnel.ufl.edu/hybrid/harris/latepoints.html This is a short review of some DSP topics relevant for speech processing. You should not use Matlab to do any of these problems however you are welcome (and encouraged) to use Matlab to check your answers.

1. In speech processing, all-pole filters are commonly used to model the human vocal tract response with the following equation:
   
   $$H(z)=\frac{1}{1-\sum_{i=1}^{p}{a_{i}z^{-i}}}$$
   
   
   Suppose the vocal tract frequency response is crudely modelled with the following second-order, causal equation:
   
   $$H(z)=\frac{1}{1+.9z^{-1}+.81z^{-2}},$$
   
   
   1. Sketch the complex plane including the unit circle with all poles and zeros of this system. Is the system stable? Explain.
   2. Derive the inverse z-transform, h[n].
2. Rectangular and Hamming windows are widely used in speech signal processing. The rectangular window is defined as follows:
   
   
   1. Use the DTFT to derive the frequency response of the rectangular window with N=9. Show all your work.
   2. Calculate the width of the main lobe of the rectangular window (hint: find the first zero).
   3. The Hamming window is defined as:
      
      If we use the same length Hamming widow (M=N), is the main lobe width the same as the rectangular window's? If yes, why? If no, what is the approximate length (M) of the new Hamming widow with the same main lobe width as the rectangular widow given in Problem 2a?
   4. For Hamming and rectangular windows of the same main lobe width, calculate the attenuation from the peak height of the main lobe to the height of the secondary lobe for each window. Express your answer in dB.
3. Glottal excitation into the vocal tract can be approximated with an impulse train.
   1. Suppose you are given a discrete-time signal containing an infinite pulse train as follows:
      
      $$e[n]= \sum_i \delta[n-i*T]$$
      
      
      where T is a positive integer. Derive and sketch the DTFT of $e[n]$ showing all of your work.
   2. Suppose you are given a continuous-time signal containing an infinite pulse train as follows:
      
      $$e(t)= \sum_i \delta(t-i*T)$$
      
      
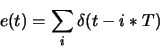
      where T is a positive real number. Derive and sketch the continuous-time Fourier Transform of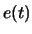 $e(t)$ showing all of your work.