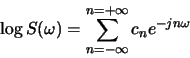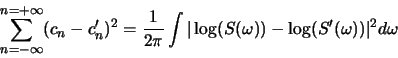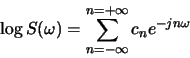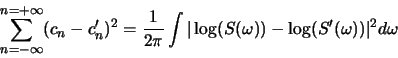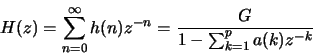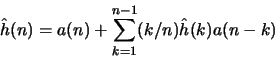Next: EEL6586: HW#5
Up: Administration
Previous: EEL6586: HW#3
Get PDF file
EEL 6586: HW#4
Assignment is due Wednesday, Feb 26, 2003 in class. Since we
will go over the assignment in class on Feb 28, late homework will not be accepted past that day. There is no matlab component of this homework.
PART A: Cepstrum Problems
- A1
- Compute the complex cepstrum of
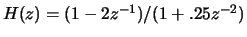
- A2
- Compute the real cepstrum of
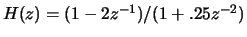
- A3
- Let
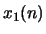 and
and 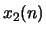 denote two sequences and
denote two sequences and 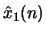 and
and 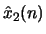 their corresponding complex cepstra. If
their corresponding complex cepstra. If
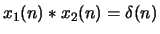 determine the relationship between
determine the relationship between
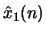 and
and 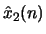 .
.
- A4
- Suppose the complex cepstrum of of
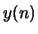 is
is
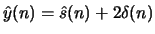 . Determine
. Determine 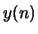 in terms of
in terms of 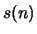 .
.
- A5
- Euclidean distance in complex cepstral space can be
related to a RMS log spectral distance measure. Assuming that
where 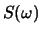 is the power spectrum (magnitude-squared Fourier
transform), prove the following:
is the power spectrum (magnitude-squared Fourier
transform), prove the following:
where 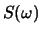 and
and 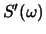 are the power spectra for two
different signals.
are the power spectra for two
different signals.
PART B: Textbook Problems
- 2.18
-
- 6.20
-
PART C: Extra Credit
Assuming that
Prove that the complex cepstrum 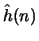 can be derived from
the linear prediction coefficients a(k) using the following
relation:
can be derived from
the linear prediction coefficients a(k) using the following
relation:
for 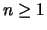 .
.



Next: EEL6586: HW#5
Up: Administration
Previous: EEL6586: HW#3
Dr John Harris
2003-04-16