


Next: EEL6586: HW#4
Up: Administration
Previous: EEL6586: HW#2
Get PDF file
EEL 6586: HW#3
Assignment is due Friday, Feb 14, 2003 in class. Late homework loses
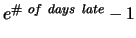 percentage
points. See the current late penalty at http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
This assignment includes both matlab and textbook questions.
PART A: Textbook problems
percentage
points. See the current late penalty at http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
This assignment includes both matlab and textbook questions.
PART A: Textbook problems
- A1
- An infinite train of impulses is created with the following relation
Assume that the sampling frequency is 10kHz.
- Determine the value of P to create a pitch frequency of 100Hz.
- The infinite train of impulses is fed through an all-pole model of
What is the dominant formant frequency in the signal?
- Is this formant frequency higher or lower than typical
first formant frequencies for humans?
- How will the formant frequency change if pre-emphasis is applied to the signal (
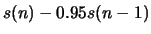 )?
)?
- A2
- Assume that an infinite impulse train
is filtered by a vocal-tract model given by
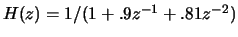 to produce a speech signal
to produce a speech signal 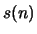 .
.
- Derive the difference equation for
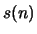 .
.
- Compute the autocorrelation function
 for the speech signal
for the speech signal 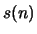 .
.
- Compute the autocorrelation function
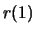 for the speech signal
for the speech signal 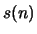 .
.
- Compute the single LPC coefficient (
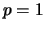 ) for this system.
) for this system.
- How does this coefficient compare to the first coefficient when
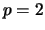 ? Explain.
? Explain.
- A3
- Assume that white noise excitation
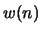 is filtered by an all-pole vocal-tract model
is filtered by an all-pole vocal-tract model
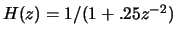 to produce a speech signal
to produce a speech signal 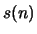 .
. 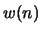 is defined:
is defined:
In this problem you will use LPC to derive an all-pole approximation to 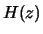 .
.
- Derive the difference equation for
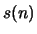 .
.
- Compute the autocorrelation function
 for the speech signal
for the speech signal 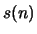 .
.
- Compute the autocorrelation function
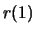 and
and
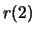 for the speech signal
for the speech signal 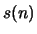 .
.
- Compute the first two LPC coefficients (
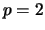 ).
).
- (5 points) Derive
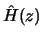 , the all-pole approximation to
, the all-pole approximation to
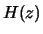 . Does your answer make sense?
. Does your answer make sense?
- A4
- Problem 5.7 in Quatieri
- A5
- (for extra credit) Prove that the 3db bandwidth of a formant caused by a single dominant pole can be approximated by
where 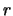 is the distance of the pole to the origin and
is the distance of the pole to the origin and  is the sampling frequency in Hz.
is the sampling frequency in Hz.
PART B: Short Answer
- B1
- Give an example of a voiced fricative and also suggest an English word that contains that voiced fricative.
- B2
- A common algorithm for pitch determination is to perform
autocorrelation on the LPC residual (error) and look for peaks. Why does
this algorithm work better than performing autocorrelation on the original
speech signal and looking for peaks?
- B3
- (5 points)
Explain what happens to your speech when you breath helium into your
vocal tract and try to speak. (Hint: the speed of sound in Helium
is about 1200m/sec).
- B4
- Explain why humans have no problem determining
the pitch of voices through the telephone, even though the cutoff
frequency is larger than typical pitch frequencies.
- B5
- A train of impulses is fed through an all-pole model of
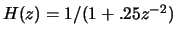 . Sketch the time domain waveform for
a few periods assuming
. Sketch the time domain waveform for
a few periods assuming  and pitch frequency is 300 Hz. Label all important parameters.
and pitch frequency is 300 Hz. Label all important parameters.
PART C: Computer Analysis of Speech
You will write a program for pitch analysis of speech. You should run your code on the sentence that you recorded
last homework as well as on the sentence found at:
http://www.cnel.ufl.edu/hybrid/courses/EEL6586/sentence.html.
You will use a pitch algorithm that takes the autocorrelation of the LPC residue for each window of speech
- C1
- Break the sentence into overlapping windows. Describe how you choose the window type, length and overlap for this pitch estimation algorithm.
- C2
- Compute the LPC coefs for each window and inverse filter the signal in that window to get the residue.
Show a typical example of the windowed signal, with plots of the time domain signal, its power spectrum, the smooth
envelope from the LPC coefs and the residue (in the time domain).
- C3
- Run an autocorrelation on the residue signal and show an example plot of the residue from [C2].
- C4
- Write a procedure that automatically computes the pitch by finding the "first biggest peak" after the lag
zero peak. What pitch is detected for your example window?
- C5
- Put all of the pieces together and write an algorithm to compute pitch for each window
Write a program that determines the pitch of each window of a sentence (if the pitch exists). Show a plot of F0 (in
Hz) vs. time (in seconds). You may need to add an additional filtering step to smooth out the pitch values. Indicate unvoiced regions and silence with a pitch of zero.
Hand in plots showing the results on the two sentences
As always, hand in all of your matlab code as
the appendix of your homework. Discuss your algorithms in detail and comment on the accuracy of your algorithms.



Next: EEL6586: HW#4
Up: Administration
Previous: EEL6586: HW#2
Dr John Harris
2003-04-16
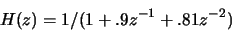
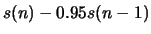 )?
)?
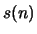 .
.
 for the speech signal
for the speech signal 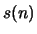 .
.
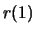 for the speech signal
for the speech signal 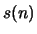 .
.
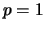 ) for this system.
) for this system.
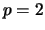 ? Explain.
? Explain.
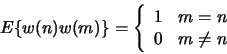
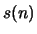 .
.
 for the speech signal
for the speech signal 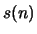 .
.
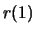 and
and
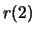 for the speech signal
for the speech signal 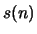 .
.
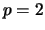 ).
).
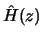 , the all-pole approximation to
, the all-pole approximation to
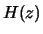 . Does your answer make sense?
. Does your answer make sense?