


Next: EEL6586: Projects
Up: EEL6586: Homework Assignments
Previous: EEL6586: HW#2
Due Wednesday, March 29, 2000 in class.
Remember that we will have an exam Wednesday, April 5, periods E1-E2, location TBA. Late
homework will lose
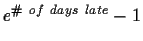 percentage points.
To see the current late penalty, click on
percentage points.
To see the current late penalty, click on
http://www.cnel.ufl.edu/analog/harris/latepoints.html
Part A: Noncomputer Problems:
-
- A1
- P7.8 in O'Shaughnessy
- A2
- P7.10 in O'Shaughnessy
- A3
- Consider a waveform quantization system with step size d(n), input
x(n), and output
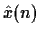 ,
where
,
where
(i.e. D is used if, in two of the last three samples, the input exceeded the
step size.). Assume that D>E>0, that d(n)=0 for 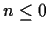 ,
and the the
sampling rate of x(n) is 10kHz.
,
and the the
sampling rate of x(n) is 10kHz.
- 1.
- What is the bit rate if this quantizer codes x(n)?
- 2.
- Is it necessary to transmit the step size as well as a coded version
of
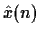 each sample instant? Explain.
each sample instant? Explain.
- 3.
- What is the maximum value that d(n) could attain? What sequence of
x(n) would lead to such a d(n)? Explain.
- 4.
- What is the minimum value that d(n) could attain? What sequence of
x(n) would lead to such a d(n)? Explain.
- 5.
- Assume that D=6, E=0, B=0.8 and
x(n)=20[u(n-3)-u(n-12)], where
u(n) is a step function. Make a table of values of x(n),
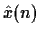 ,
and d(n) for
,
and d(n) for
 .
.
Part B: Computer Problems:
You will design a simple LPC10-like quantizer for this part. You do
not need to find out the exact details of the LPC-10e standard, if fact I
would rather that you not. You will demonstrate your coder on the
standard sentence at:
http://www.cnel.ufl.edu/analog/courses/EEL6586/sentence.html.
Explain your reasoning for each step of the design.
- B1
- Perform LPC analysis on the framed sentence.
Use which ever order you
think is best for minimizing the bitrate while preserving
intelligibility.
- B2
- Decide voiced vs. unvoiced for each window using any procedure you
like. Show a plot showing the voiced vs. unvoiced regions for the
sentence.
- B3
- If the window is voiced, determine the appropriate pitch period. Show
a plot indicating how pitch changes vs. time for this sentence. (You should already have this code from HW#2).
- B4
- Synthesize the full sentence using only the LPC, pitch, and voiced
vs. unvoiced information.
Is the speech intelligible? i.e. would the speech be
understood by someone who has never
heard the sentence before? Mail the synthesized .wav file to Dr. Harris.
- B5
- Synthesize another sentence of your own choosing. Also mail, these wave files to Dr. Harris (original and synthesized). How well does your coder work?
As always turn in all of your matlab code and explain all of your work. Don't forget to email the three .wav files that were requested.



Next: EEL6586: Projects
Up: EEL6586: Homework Assignments
Previous: EEL6586: HW#2
Dr John Harris
2000-04-19
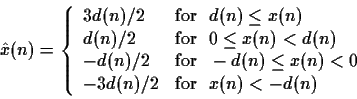
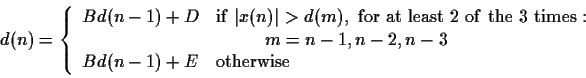
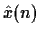 each sample instant? Explain.
each sample instant? Explain.
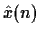 ,
and d(n) for
,
and d(n) for
 .
.