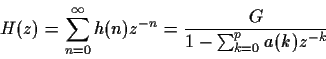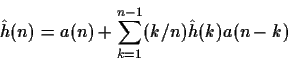Next: EEL6586: HW#3
Up: EEL6586: Homework Assignments
Previous: EEL6586: HW#1
Due Wednesday, March 15, 2000 in class. No electronic submissions, only hardcopies. Late
homework will lose
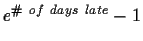 percentage points.
To see the current late penalty, click
percentage points.
To see the current late penalty, click
http://www.cnel.ufl.edu/analog/harris/latepoints.html
PART A: Noncomputer Problems
- A1
- (10%) 6-parameter LPC analysis was performed on a voiced phoneme
recorded with fS=10kHz. The resulting pole/zero plot is as shown in
the following figure:
Estimate which phoneme was recorded. List the proper symbol of the phoneme and
explain your reasoning.
- A2
- (10%) Compute the complex cepstrum of
H(z)=1+z-2
- A3
- (30%)
Consider the infinite-length signal x(n), a short segment is shown above.
Your goal is to derive the LPC coefficients
for the prediction of x(n). Assume order p=2 (that is, you will only
consider the two previous values in predicting the next one).
- (a)
- Compute the autocorrelation matrix R
and the cross correlation vector
 .
(Assume an extremely long
window and include a 1/N normalization factor).
.
(Assume an extremely long
window and include a 1/N normalization factor).
- (b)
- Compute the LPC coefficients and the resulting error in prediction.
- (c)
- Sketch the magnitude response of the all-pole estimator for this signal (H(z)).
PART B: Computer Analysis of Speech
You will write two programs for speech analysis. You should run your code on a sentence that you record as well as on
the sentence found at:
http://www.cnel.ufl.edu/analog/courses/EEL6586/sentence.html.
- B1
- (25%) Write a program that determines the pitch of a signal (F0
in Hz.) We talked about a number of algorithms in class but one of the autocorrelation techniques would be straightforward to implement.
- B2
- (25%) Write a program that determines the first three formant
location (F1, F2, F3 in Hz.) We will talk in class about several techniques
but factoring the LPC polynomial is probably the most straightforward.
As always, hand in all of your matlab code. Discuss your algorithms in
detail and hand in plots showing the results on the two sentences. Comment
on the accuracy of your algorithms.
PART C: Extra Credit
(5%) Assuming that
Prove that the complex cepstrum
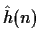 can be derived from the linear
prediction coefficients a(k) using the following relation:
can be derived from the linear
prediction coefficients a(k) using the following relation:
for 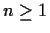 .
.



Next: EEL6586: HW#3
Up: EEL6586: Homework Assignments
Previous: EEL6586: HW#1
Dr John Harris
2000-04-19
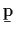 .
(Assume an extremely long
window and include a 1/N normalization factor).
.
(Assume an extremely long
window and include a 1/N normalization factor).