![]()
The adaptive filter that is used to model H(z) has two free parameters, a and b, as follows:
![]()
The input to both systems is unit variance white noise and the goal is to
find the values of a and b that minimize the mean-square error
( ![]() ).
).
- (optional) The mean-square error is a bimodal function for the given parameters. Show how to derive the numerical values for a and b for the global minimum and for the local minimum. (Answer: global minimum at (a,b)=(-.311,0.906) and local minimum at (0.114,-0.519)).
- Write down the equations for the simplified IIR LMS adaptive filter.
- Write down the equations for the filtered signal approach LMS adaptive filter.
-
A further simplification that has been proposed by Feintuch is to ignore the
feedback terms in the equations for the gradient estimates. This
simplification results in:
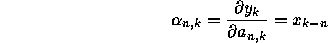
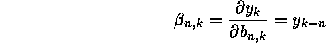
Although more efficient than the filtered signal approach, this algorithm may converge to a false minimum, even when the simplified IIR LMS algorithm and the filtered signal approach converge to a minimum. Write down the adaptive filtering equation for W(z) using Feintuch's algorithm.
-
In order for the filter coefficients
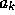 and
and 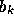 in W(z) to converge in
the mean using Feintuch's algorithm, it is necessary that
in W(z) to converge in
the mean using Feintuch's algorithm, it is necessary that

and
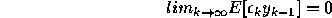
Find the values of
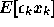 and
and  at the global minimum. What
does this imply about Feintuch's algorithm?
at the global minimum. What
does this imply about Feintuch's algorithm? -
Find the stationary point of the Feintuch adaptive filter, i.e., the value
or values of a and b for which
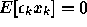 and
and
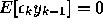 .
.
![]()
![]()
where
![]()
is the error signal that has been filtered with an FIR filter C(z). Suppose that the coefficients of a second-order adaptive filter
![]()
are updated using the SHARF algorithm with
![]()
- Write down the SHARF adaptive filter equations for H(z).
- If the SHARF algorithm converges in the mean, then
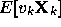 converges to zero, where
converges to zero, where
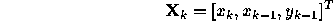
What does this imply about the relationship between the filter coefficients
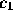 and
and 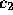 and
and 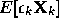 ?
? - What does the SHARF algorithm correspond to when c(z)=1?
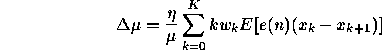
Refer to the paper by Principe et al. for the full description and notation for the gamma filter.