


Next: EEL6502: HW6
Up: EEL6502: Homeworks
Previous: EEL6502: HW4
Due Wednesday, April 10 in class at 3pm. Late homework will not be
accepted.
-
Once again, consider the adaptive noise cancellation problem where the
primary signal is zero-mean Gaussian noise with variance
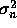 (
( 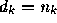 ) and the reference signal is equal to one (
) and the reference signal is equal to one ( 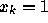 ). Remember
that you only need one tap weight for this problem. Suppose someone decides
to implement a variable step rate algorithm where
). Remember
that you only need one tap weight for this problem. Suppose someone decides
to implement a variable step rate algorithm where 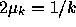 for
k>0. Derive an exact expression for the variance of the weight value as a
function of k. Discuss the significance of this result.
for
k>0. Derive an exact expression for the variance of the weight value as a
function of k. Discuss the significance of this result. - Consider the homogeneous problem
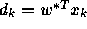 , where
, where
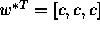 (assume c>0) and where
(assume c>0) and where 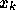 is the 3-periodic sequence
is the 3-periodic sequence
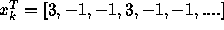 Initialize the weights to zero.
Initialize the weights to zero.
- Show that the Sign-Sign algorithm
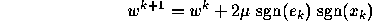
is always divergent in the sense that
 (
( 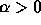 )
)
- Find limits on
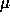 for the conventional LMS algorithm to converge.
for the conventional LMS algorithm to converge.
- Show that the direct minimization of
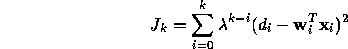
leads to

where
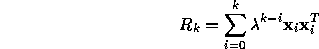
and

- (Extra Credit) Prove the matrix inversion lemma. This lemma was
discussed in class and is also listed in the handout from Clarkson's book.
(turn over)
- The rest of this assignment
deals with a very simplified filter design problem. We would like
to reject frequencies at f2 while preserving the signals at surrounding
frequencies of f1 and f3. We will generate the data using
the following code in MATLAB
isize=300; basis=1:isize; %change isize to whatever length you need;
d=.1*randn(1,isize);x=.1*randn(1,isize);
f1=1/100; f2=sqrt(2)/100; f3=sqrt(3)/100;
for f= [f1 f2 f3] x=x+sin(2*pi*f* 1:isize); end
for f= [f1 f3] d=d+sin(2*pi* 1:isize); end
Estimate the speed of convergence of the LMS algorithm as a function of 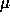 assuming two taps.
You may use MATLAB to verify your result.
assuming two taps.
You may use MATLAB to verify your result. - Estimate the speed of convergence in the limit of a very
large number (L+1)
taps. (You should not have to run a program to get this value)
- Estimate the speedup you expect from using RLS for this
problem for (a) 2 taps (b) many taps. Explain.
The remaining questions must be answered with MATLAB or similar program.
- Choose reasonable values for
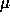 and the number of taps and run the
LMS algorithm you have used in previous assignments. Give analytic and
measured values of convergence rate and misadjustment for the value of
and the number of taps and run the
LMS algorithm you have used in previous assignments. Give analytic and
measured values of convergence rate and misadjustment for the value of 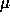 and the number of taps you choose you choose.
and the number of taps you choose you choose. - Implement the RLS algorithm (either the standard or the exponentially
weighted version) and solve the same filter design problem
given above. Compare the
misadjustment and convergence rates to that of the LMS implementation.
- Show the frequency plots for the desired and filter outputs.
Plot the frequency response for the filter that you come up with (this does
not mean to just plot the fft of
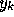 ). Does this method succeed in
blocking signals at f2 while keeping signals at f1 and f3?
). Does this method succeed in
blocking signals at f2 while keeping signals at f1 and f3?



Next: EEL6502: HW6
Up: EEL6502: Homeworks
Previous: EEL6502: HW4
Dr John Harris
Fri Feb 6 11:05:57 EST 1998
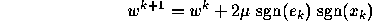
 (
( 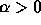 )
)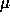 for the conventional LMS algorithm to converge.
for the conventional LMS algorithm to converge.
![]()
![]()
![]()
![]()