EEL6502: HW3

Due Monday February 19 in class at 3pm. Late homework will not be accepted.

 
Figure 1:   Adaptive Filter Architecture for Single Step Prediction

This assignment will explore theory vs. practice for the linear prediction problem using the LMS algorithm. Make reasonable assumptions and explain your work. A second-order autoregressive (AR) process is described by

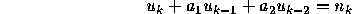
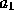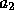where and are real-valued constant coefficients, and 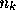is a white noise process with zero mean and a variance of one. We use the adaptive filter depicted above to predict the next value of the series using the previous two values (i.e. there is a single delay in the adaptive filter and two weights).

Express each of the following in terms of the AR parameters 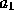and .

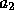A1

The simplest prediction value is to guess the mean value at each iteration, i.e. 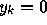. What is the value of the MSE for this predictor?

A2

Another simple estimator is to guess the previous value i.e. 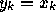. What is the value of the MSE for this predictor?

A3

Derive the optimal Wiener Filter weights 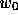and .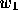

A4

What is the MSE for the Wiener Filter? Can the MSE computed above be reduced by adding more taps? Explain.

A5

Compute the autocorrelation function 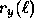. Explain the significance of this result.

Let 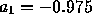and . Give numerical values for the following questions; you do not need a computer.

B1

Compute the eigenvectors and eigenvalues of the R matrix.

B2

Use the results from B1 to come up with an upper bound on the value of 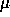to guarantee convergence in the mean.

B3

Give values of 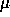that provide misadjustment values of 5% and 1%

B4

Estimate the expected number of iterations for the mean convergence of the MSE for these two values of 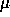. Assume four time constants or a similar definition for convergence.

B5

Compute the expected variance of the final weight values.

Do the following parts using Matlab (or similar program).

C1

Compute the numerical value of the MSE for the predictor 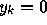. Compare to the value you computed in A1.

C2

Compute the numerical value of the MSE for the predictor 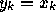. Compare to the value you computed in A2.

C3

Write an LMS routine to do linear prediction using two taps. For input use the second order AR process with parameters 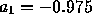and . You will use the two values of 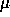you computed in B3. Hand in plots that show the following:

• Plot the value of 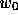vs. k for the two values of .
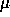• Plot the value of 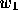vs. k for the two values of .
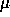• Plot the value of MSE vs. k for the two values of .

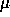How does the measured variance of the weights compare to the value you computed in B5?

C4

Draw the same plots as in C3, but this time do an ensemble average of at least 200 runs to get smoother curves for each plot. How do the final weight values compare to the values you computed in A3? How does the final MSE relate to the value you computed in A4? How does the convergence rate of the program compare to the expected value you computed in B4?

C5

What is the maximum value of 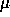you can use that keeps the weight values from exploding? How does this value compare to what you computed in question B2. Explain why they are different.