


Next: EEL6502: HW3
Up: EEL6502: Homeworks
Previous: EEL6502: HW1
Due Monday February 5 in class at 3pm. Late homework will not be
accepted. Anytime you use Matlab (or similar program) you should
hand in all of the files you used to generate your answers.
- Do problems 4 and 5 in Chapter 4 in Widrow & Stearns.
The rest of this assignment deals with searching the 2D performance
surface for problem shown in Figure 2.6 in the book. We will use N=4.9626
throughout.
Do the following parts without using Matlab:
- Compute numerical values for R, p and
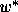 .
. - Derive numerical values for the eigenvalues and eigenvectors of R.
- Write R in normal form (i.e. diagonalized form)
using the eigenvalues and eigenvectors in question 3.
- Choose a value of the step size parameter
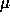 for which for gradient descent search is overdamped for both
dimensions. Call this value
for which for gradient descent search is overdamped for both
dimensions. Call this value 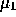 .
. - Choose a value of the step size parameter
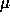 for which for gradient descent search is underdamped for both
dimensions. Call this value
for which for gradient descent search is underdamped for both
dimensions. Call this value 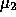 .
. - Derive the optimal value of
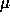 as discussed in class.
Call this value
as discussed in class.
Call this value 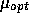 .
.
Do the following parts using Matlab.
- Create data vectors 1000 elements long for
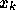 and
and 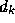 . If you
have questions on how to create these vectors, you can refer to the file
hw2_dat.mat in the course ftp directory.
. If you
have questions on how to create these vectors, you can refer to the file
hw2_dat.mat in the course ftp directory. - Use the functions you wrote from hw1 and verify that the computed
R, p and
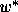 correspond to the analytic values derived in question 3.
correspond to the analytic values derived in question 3. - Implement the simple gradient descent search using the known form of
the gradient. Iterate the solution until a suitable MSE value is reached.
Plot the MSE vs. iteration number on a linear plot for all three values of
mu.
- Use Matlab to create a contour plot showing several ellipses of constant MSE.
- On the contour plot, show the convergence of the gradient descent
procedure using each value of
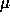 .
The plot should resemble that shown in Figure 4.7
in the book.
.
The plot should resemble that shown in Figure 4.7
in the book. - Plot the MSE vs. iteration number on a semilogy plot for each
case. Does the measured slope near zero MSE correspond to the value you
expect in each case? Explain.



Next: EEL6502: HW3
Up: EEL6502: Homeworks
Previous: EEL6502: HW1
Dr John Harris
Fri Feb 6 11:05:57 EST 1998