EEL6935: HW#1

Due Thursday, July 6 at 5pm. Late homework will lose 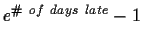$e^{\char93 ~of~days~late} -1$ percentage points. Click on http://www.cnel.ufl.edu/analog/harris/latepoints.html to see the current late penalty.

PART A: Intensity and Loudness - Hand Analysis (20 points)

Suppose a loudspeaker is playing a continuous 4KHz tone which measures 50dB SPL at a distance of one meter. Answer each of the following independent questions, be sure to explain your answers.

A1

If the intensity of the tone is doubled, how many decibels does it now measure? Explain.

A2

If the intensity of the tone is doubled, how many times louder does it now sound? Explain.

A3

If the loudspeaker plays an additional, simultaneous 40dB tone at 900Hz, what is the measured intensity of the combined signal? Explain.

A4

About how far can we move the speaker before YOU probably couldn't hear the 4KHz tone any more. Explain your reasoning and any assumptions you make.

PART B: Critical Bandwidth - Hand Analysis (30 points)

One approximation for the critical bandwidth is given by the Cambridge equation:

B_C=24.7(1+4.37F)

where B_C is the equivalent rectangular (ERB) bandwidth in Hz and F is the center frequency in kHz. Answer the following questions.

B1

Over the range of center frequencies from 50Hz to 10kHz, what is the maximum and minimum Q values of the filters?

B2

The nervous system essentially implements a continuous band of frequencies but how many discrete ERB filters would it take to fill the range from 50Hz to 10kHz when they are placed edge to edge?

B3

Usually these filters are approximated by a bank of filters that are each 1/3 octave in width over the full frequency range. Design an nth-order Butterworth filter that is 1/3 octave in width, given the order n of the filter and the center frequency.

B4

How many of these nth-order Butterworth filters from [B3] would it take to fill the range from 50Hz to 10kHz? Assume that the filters are placed so that they intersect at their 3dB points.

B5

Discuss the length of the impulse response for the nth-order Butterworth filters from [B3]. How does the length change with frequency? Why is this important? Can you derive an exact expression for the impulse response or its length?

PART C: Temporal Integration - Computer Analysis (50 points)

In this part, you will simulate the temporal integration and detection experiments in matlab.

C1

Create a synthetic segment of sound consisting of pure white noise over the full range with a single sinusoid at 1KHz superimposed during a short interval. Set things up so that the sine wave is just audible. Explain how you do this.

C2

Design a detection algorithm consisting of a bandpass filter (1/3 octave), rectification, leaky integration and simple thresholding. Include your matlab code in what you turn in. Explain your design.

C3

Tweak your threshold of detection and your time constant so that you roughly match your performance in terms of signal amplitude and duration. Guage your performance by listening to various lengths of the sine wave over your PC speakers or headphones. Explain how you do this and what your final values are. If you can think of better ways to try different approaches to find these parameters.

C4

Plot the signal amplitude (in dB) just necessary for detection vs. duration length on a log time scale. Hand in a properly labeled graph showing your results.