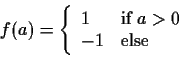Next: EEL6825: Homework Solutions
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#3
Due Friday, November 12, 1999 in class. This is your final homework of
the semester. Late homework will lose
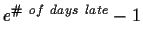 percentage
points. To see the current late penalty, click
http://www.cnel.ufl.edu/analog/harris/latepoints.html
percentage
points. To see the current late penalty, click
http://www.cnel.ufl.edu/analog/harris/latepoints.html
PART A: Textbook Problems
Answer the following questions, you should not use a computer.
- A1
- (5 points)
Class 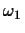 points are:
points are:
Class 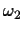 points are:
points are:
Find any weight vector w such that
wTx>0 for all class 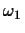 points and
wTx<0 for all class
points and
wTx<0 for all class 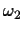 points. Justify your answer.
points. Justify your answer.
- A2
- (5 points)
The density function of a two-dimensional random vector x consists of four
impulses at (0,3) (0,1) (1,0) and (3,0) with probability of 1/4 for each.
Find the K-L expansion. Compute the mean-square error when one feature is
eliminated. Compute the contribution of each point to the mean-square error.
- A3
- (5 points) In one paragraph, compare the three types of
classifiers we have discussed in the class (parametric, nonparametric and
neural networks). Contrast them in terms of training time, testing time,
and the number of data points required.
PART B: KL and Continuous Distribution
You are given two three-dimensional normal
distributions with the following means and
covariance matrices:
![$\mu_1=
\left[
\begin{array}{c}
-1 \\
1 \\
0
\end{array}\right]
$](img34.gif)
![$\mu_2=
\left[
\begin{array}{c}
1 \\
-1 \\
0
\end{array}\right]
$](img35.gif)
![$\Sigma_1=
\left[
\begin{array}{ccc}
1&0&0 \\
0&1&0 \\
0&0&0
\end{array}\right]
$](img36.gif)
![$\Sigma_2=
\left[
\begin{array}{ccc}
5&2&0 \\
2&1&0 \\
0&0&0
\end{array}\right]
$](img37.gif)
Assume that
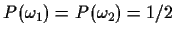 Answer the following questions
relating to using the K-L transform for dimensionality reduction.
Answer the following questions
relating to using the K-L transform for dimensionality reduction.
- B1
- (5 points)
Compute the combined mean (
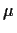 )
and covariance matrix (
)
and covariance matrix (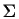 )
for the
data in this problem.
Hint: Remember that the combined distribution of two equally likely
normal distributions
is not a normal distribution but the combined covariance matrix
can be expressed as:
)
for the
data in this problem.
Hint: Remember that the combined distribution of two equally likely
normal distributions
is not a normal distribution but the combined covariance matrix
can be expressed as:
- B2
- (5 points)
Compute all of the eigenvalues and eigenvectors of
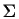 .
.
- B3
- (5 points)
If you had to drop one linear feature, which eigenvalue direction would you
drop? Comment on the likely resulting change (if any) in the error for
representation and for classification.
- B4
- (5 points)
If you had to drop two linear features, which
two eigenvalue directions would you
drop? Comment on the likely resulting change (if any) in the error for
representation and for classification.
- B5
- (5 points)
Draw a very rough sketch 2-D sketch of the two distributions and show the
key linear features under consideration. You do not have to draw exact
equiprobability contours for each distribution. Make clear which direction
you are deciding to keep (from your answer to part B4).
PART C: Neural Networks
Consider the following sample points:
The samples from class 1 are:
![$
\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]
\left[ \begin{array}{c} 1 \...
... \\ 1 \end{array} \right]
\left[ \begin{array}{c} -1 \\ -1 \end{array} \right]
$](img42.gif) The samples from class 2 are:
The samples from class 2 are:
![$
\left[ \begin{array}{c} 0 \\ 2 \end{array} \right]
\left[ \begin{array}{c} 2 \...
...2 \\ 0 \end{array} \right]
\left[ \begin{array}{c} 0 \\ -2 \end{array} \right]
$](img43.gif)
Answer the following questions regarding the neural network solution to this problem.
- C1
- (5 points) How many hidden nodes are required to solve this problem? Explain.
- C2
- (5 points)
Assume the sigmoid activation function of the neural network to be:
Derive a neural network architecture that solves this problem.
The final output of your neural network should be
+1 for class 1 and -1 for class 2.
Provide all of the necessary
weight values for architecture with the minimum
number of hidden units. Explain your reasoning and justify your results.
- C3
- (5 points) The hard limiting step function in [C2] is not used in
practice. Explain why not.
- C4
- (50 points) Program a backpropagation algorithm to solve this
problem. Use the same architecture that you came up with in [C2] only
with a different sigmoid. Make sure that you initialize your weights with
small random values. Show a few plots of MSE vs. iteration number.
- C5
- (5 points) Hand in a plot of the decision boundaries for class 1 and
class 2 along with the data points. There should be no errors. Note: it
may be helpful for you to periodically plot these regions as the algorithm
is running to see how far you are away from the correct solution.
As usual, include all plots and answers to questions in the first part of
your document. All matlab code that you write should be included in the
second part.



Next: EEL6825: Homework Solutions
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#3
Dr John Harris
1999-12-10
![]() points are:
points are:
![\begin{displaymath}\left[
\begin{array}{c}
-1 \\
-1 \\
+1
\end{array}\right]
\...
...t]
\left[
\begin{array}{c}
+1 \\
-1 \\
-1
\end{array}\right]
\end{displaymath}](img32.gif)
![]() points are:
points are:
![\begin{displaymath}\left[
\begin{array}{c}
+1 \\
+1 \\
-1
\end{array}\right]
\...
...t]
\left[
\begin{array}{c}
-1 \\
+1 \\
+1
\end{array}\right]
\end{displaymath}](img33.gif)
![]() points are:
points are:
![\begin{displaymath}\left[
\begin{array}{c}
-1 \\
-1 \\
+1
\end{array}\right]
\...
...t]
\left[
\begin{array}{c}
+1 \\
-1 \\
-1
\end{array}\right]
\end{displaymath}](img32.gif)
![]() points are:
points are:
![\begin{displaymath}\left[
\begin{array}{c}
+1 \\
+1 \\
-1
\end{array}\right]
\...
...t]
\left[
\begin{array}{c}
-1 \\
+1 \\
+1
\end{array}\right]
\end{displaymath}](img33.gif)
![$\mu_1=
\left[
\begin{array}{c}
-1 \\
1 \\
0
\end{array}\right]
$](img34.gif)
![$\mu_2=
\left[
\begin{array}{c}
1 \\
-1 \\
0
\end{array}\right]
$](img35.gif)
![$\Sigma_1=
\left[
\begin{array}{ccc}
1&0&0 \\
0&1&0 \\
0&0&0
\end{array}\right]
$](img36.gif)
![$\Sigma_2=
\left[
\begin{array}{ccc}
5&2&0 \\
2&1&0 \\
0&0&0
\end{array}\right]
$](img37.gif)
![]() Answer the following questions
relating to using the K-L transform for dimensionality reduction.
Answer the following questions
relating to using the K-L transform for dimensionality reduction.
![$
\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]
\left[ \begin{array}{c} 1 \...
... \\ 1 \end{array} \right]
\left[ \begin{array}{c} -1 \\ -1 \end{array} \right]
$](img42.gif) The samples from class 2 are:
The samples from class 2 are:
![$
\left[ \begin{array}{c} 0 \\ 2 \end{array} \right]
\left[ \begin{array}{c} 2 \...
...2 \\ 0 \end{array} \right]
\left[ \begin{array}{c} 0 \\ -2 \end{array} \right]
$](img43.gif)