


Next: EEL6825: Projects
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#4
 EEL 6825 - Fall 1997
EEL 6825 - Fall 1997
Due Wednesday, Nov. 19 at 3pm. This is your last homework of the
semester. Exam 2 is Monday, Nov. 24 and the review for the
exam is on Friday, Nov. 21.
PART A: Non-computer questions
- A1
- Describe the smallest MLP neural network you can think of that
will correctly classify points (0,1) and (1,0) as class 1 and points (0,0)
and (1,1) as class 2. What is the exact configuration and weight values that
you use?
- A2
- Consider a simple example of a network involving a single weight
for which the cost function is
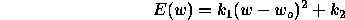
where 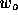 ,
,
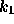 , and
, and 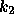 are constants. A backpropagation algorithm with momentum is
used to minimize E(w). How does the momentum constant
are constants. A backpropagation algorithm with momentum is
used to minimize E(w). How does the momentum constant 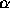 change the
convergence rate for this system? Explain.
change the
convergence rate for this system? Explain.
- A3
-
Suppose a student is given data that consists of many 2-D samples of the 1-D
curve described by:
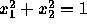 where
where 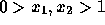 . Why can't the
standard K-L transform accurately represent this data in one dimension?
Sketch the likely result of using the K-L transform to reduce the dimension
for this problem.
. Why can't the
standard K-L transform accurately represent this data in one dimension?
Sketch the likely result of using the K-L transform to reduce the dimension
for this problem.
- A4
-
The density function of a two-dimensional random vector x consists of four
impulses at (0,3) (0,1) (1,0) and (3,0) with probability of 1/4 for each.
Find the K-L expansion. Compute the mean-square error when one feature is
eliminate. Compute the contribution of each point to the mean-square error.
PART B: Computer questions
- B1
-
Load the data from the files
http://www.cnel.ufl.edu/analog/courses/EEL6825/xarray.asc
and
http://www.cnel.ufl.edu/analog/courses/EEL6825/darray.asc
The xarray consists of a list of two-dimensional data points and the darray
contains the corresponding class labels (either +1 or -1). Develop a
multi-layer perceptron architecture and algorithm that can classify the
data. Plot the decision boundary used by the network.
How does the error change with the number of hidden nodes?
- B2
- Reduce the dimensionality of the sonar data (from HW#4)
using the K-L Transform.
Obviously, you must use exactly the same linear transform on both classes.
Build a nearest neighbor classifier in this reduced dimension space. How
does the resulting 1-NN leave-one-out error change with dimensionality?
Explain your observations.
- B3
- Extra credit. Run your neural network algorithm on the reduced
dimensionality rocks/mines problem. How does your error compare to the
nearest neighbor solution?



Next: EEL6825: Projects
Up: EEL6825: Homework Assignments
Previous: EEL6825: HW#4
Dr John Harris
Mon Nov 10 01:03:10 EST 1997
![]() EEL 6825 - Fall 1997
EEL 6825 - Fall 1997
![]()
![]() ,
,
![]() , and
, and ![]() are constants. A backpropagation algorithm with momentum is
used to minimize E(w). How does the momentum constant
are constants. A backpropagation algorithm with momentum is
used to minimize E(w). How does the momentum constant ![]() change the
convergence rate for this system? Explain.
change the
convergence rate for this system? Explain.