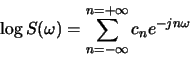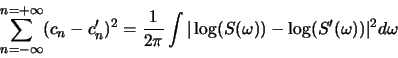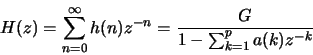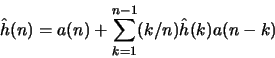Next: EEL6586: HW#4
Up: EEL6586: Homework
Previous: EEL6586: HW#2
Get PDF file
EEL 6586: HW#3
Assignment is due Friday, March 9, 2007 in class. Late
homework loses
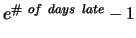 percentage
points. This assignment includes
both Matlab and textbook questions.
Remember that the Exam will be periods E2-E3 on March 22, room TBA. Let the instructor know asap if you have a conflict
PART A: Short Answer (No more than a few sentences each)
percentage
points. This assignment includes
both Matlab and textbook questions.
Remember that the Exam will be periods E2-E3 on March 22, room TBA. Let the instructor know asap if you have a conflict
PART A: Short Answer (No more than a few sentences each)
- A1
- Compute the complex cepstrum of
Assume 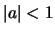 .
.
- A2
- Compute the complex cepstrum of
Assume 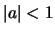 .
.
- A3
- Compute the real cepstrum of
Assume 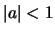 .
.
- A4
- Can we invert the Mel Frequency Cepstrum? Explain.
- A5
- Explain how cepstral mean subtraction can get rid of fixed convolution artifacts due to various environmental and microphone transfer functions.
PART B: Textbook problems (Use Matlab only to optionally check your work)
- B1
- Compute the complex cepstrum of the following causal filter
- B2
- Assume that a signal
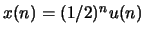 is fed into the filter
is fed into the filter 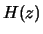 given in B1 to produce
given in B1 to produce 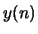 . What is the complex cepstrum of
. What is the complex cepstrum of 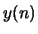 ?
?
- B3
- Compute the complex cepstrum of
 for
for 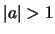 (nonminimum phase).
(nonminimum phase).
- B4
- Euclidean distance in complex cepstral space can be
related to a RMS log spectral distance measure. Assuming that
where 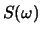 is the power spectrum (magnitude-squared Fourier
transform), prove the following:
is the power spectrum (magnitude-squared Fourier
transform), prove the following:
where 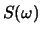 and
and 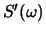 are the power spectra for two
different signals.
are the power spectra for two
different signals.
- B5
- Assuming that
Prove that the complex cepstrum 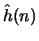 can be derived from
the linear prediction coefficients a(k) using the following
relation:
can be derived from
the linear prediction coefficients a(k) using the following
relation:
for 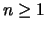 .
.
PART C: Phoneme Recognition Experiments in Matlab
Utterances of 8 vowel phonemes from 38 speakers from the TIMIT
database were extracted (about 2300 utterances total). Your goal
for this problem is to achieve the highest recognition accuracy
for this speech corpus. In the end you are free to do whatever
you can to improve recognition accuracy. A demo Matlab program
using LPC-10 and 1-NN is provided to demonstrate usage of the
database. The following files are provided:
hw3Data.mat:
Matlab .mat file containing the variables vocab, *Utter, and
*Speaker, where * is one of the phonemes in vocab. *Utter is a
512xN (N varies w/ phoneme) matrix where each column is a 512-pt
utterance extracted from the center (to minimize coarticulation
effects) of a labeled phoneme from the TIMIT database. *Speaker is
an Nx5 character matrix w/ each row i is the speaker label for
column i in *Utter. *Speaker is provided to ensure that no
speaker appears in both the test/train sets. about 9MB
uncompressed.
hw3Demo.m:
Matlab .m file that demonstrates usage of hw3Data.mat. LPC coeffs
are extracted in bulk, random test/train speakers are designated
for each classifier trial, and the test/train LPC coeffs are used
w/ a 1-Nearest Neighbor classifer. Run this program to make sure
you have downloaded the database properly. Tweak the following
variables to see their effects on accuracy: percentTest,
numTrials, vocab (you can shrink the vocab as a sanity check that
your program works properly-small vocab means high recognition
accuracy). Feel free to modify this code when writing your own
solution.
hw3Readme.txt:
Readme file that describes all files in hw3.zip.
All these files are conveniently available in hw3.zip which can be
found at:
http://www.cnel.ufl.edu/hybrid/courses/EEL6586/hw3.zip
- C1
- Choose a robust feature extraction technique that you
think will provide best results. You may use any feature
extraction techniques you want (energy, zero-crossing, LPC, mfcc,
PLP, hfcc...) or any combination of these. You are free to look at
several different types of feature sets or to invent your own but
do whatever you can to improve the recognition accuracy (without
using test data during training). Explain your choice of feature
set and why you think that it should perform well.
- C2
- Use a classification algorithm to classify the test
data. Again you are free to use any classifier you like (Nearest
Neighbor, Bayes, Neural Network, HMM, ...) Briefly explain why
your choice of a classifier is a wise one (even if you decide to
stay with the nearest neighbor classifier).
- C3
- Always include several trials as in hw3Demo.m and report
the average over all trials. For your final version, make sure to
include at least 100 trials. What is your final accuracy rate?
What is the standard deviation of your accuracy value?
- C4
- For your final optimized system, which two phonemes are
most likely to be confused with one another?
- C5
- Comment on why it is important that no speaker appear in
both the test/train datasets.
As usual, attach all of your code to the end of the assignment. Bonus points will be awarded to the person(s) with the
highest percentage correct classification.



Next: EEL6586: HW#4
Up: EEL6586: Homework
Previous: EEL6586: HW#2
Dr John Harris
2007-04-09