- a)
- Compute the complex cepstrum
of
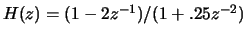
- b)
- Compute the real cepstrum of
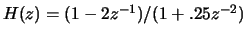
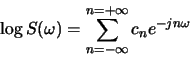
where
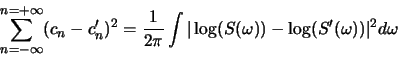
where
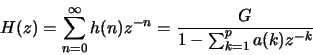
Prove that the complex cepstrum
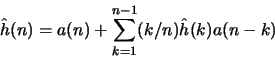
for
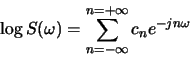
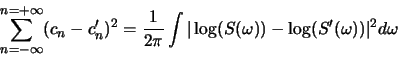
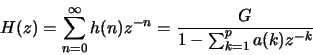
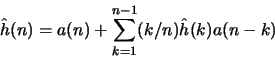
![\begin{displaymath}A_e=A_o=A=\{a_{ij}\}= \left[
\begin{array}{cc}
.9&.1 \\
0&1
\end{array}
\right] \end{displaymath}](img37.gif)
![$B_e=\{b_{i}(k)\}= \left[
\begin{array}{cc}
.8&.7 \\
.1&.1 \\
.1&.2
\end{array}
\right] $](img38.gif)
![$B_o=\{b_{i}(k)\}= \left[
\begin{array}{cc}
.2&.1 \\
.4&.3 \\
.4&.6
\end{array}
\right] $](img39.gif) The columns of the B matrix denote the probabilities of the three symbols (
The columns of the B matrix denote the probabilities of the three symbols (ti\_00F8ST01) as well as the class (digit) each one classified as. Comment on possible
explanations as to why these utterances were misclassified.
% Create random sequence of normal distribution (zero mean, unity variance): noise = randn(size(x)); % x is the "clean" time-domain utterance (whole word) % Find energy of each utterance and noise: energyX = sum(x.^2); energyNoise = sum(noise.^2); % Find amplitude for noise: noiseAmp = sqrt(energyX/energyNoise*10^(-SNR/10)); % SNR is in dB % Add noise to utterance: x = x + noiseAmp*noise;