


Next: EEL6586: HW#2
Up: EEL6586: Homework
Previous: EEL6586: Homework
Get PDF file
EEL 6586: HW#1
Assignment is due Friday, January 13, 2004 in class. Late
homework loses
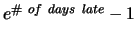 percentage
points. See the current late penalty at http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
This is a short review of some DSP topics relevant for speech
processing. You should not use Matlab to do any of these problems
however you are welcome (and encouraged) to use Matlab to check
your answers.
percentage
points. See the current late penalty at http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
This is a short review of some DSP topics relevant for speech
processing. You should not use Matlab to do any of these problems
however you are welcome (and encouraged) to use Matlab to check
your answers.
- (25 points)
A stable digital filter has the following transfer function
- (5 points) Derive the poles and zeros of
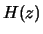 and sketch
them on a pole/zero plot. State the ROC.
and sketch
them on a pole/zero plot. State the ROC.
- (20 points) Derive a stable
![$h[n]$](img4.gif) from the given
from the given 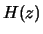
- (25 points) You are given the following difference equation:
![\begin{displaymath}
y_1[n]=x[n]+2y_1[n-1]-2y_1[n-2]
\end{displaymath}](img5.gif) |
(1) |
![\begin{displaymath}
y_2[n]=y_1[n]-y_1[n-1]
\end{displaymath}](img6.gif) |
(2) |
- (5 points) Derive
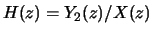
- (10 points) Derive a causal impulse response
![$h[n]$](img4.gif) .
.
- (10 points) Provide a new set of difference equations (to
replace (1) and (2) on the last page) such that a stable and
causal system exists that has the same magnitude response as
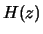 . (Note: you can do this part even if you are not able to
complete part b).
. (Note: you can do this part even if you are not able to
complete part b).
- (25 points) A generalized linear, FIR, causal filter has
zeros at the following locations: 1, -1, and 1/2. (hint: some of
these can be multiple zeros and there can be zeros at other
locations).
Answer the following questions (hint: you can answer them in any
order)
- (5 points) What other zero must be present if this filter is
one of the four filter types (I-IV)?
- (5 points) Can this filter be type I? Either give an example
impulse response
![$h[n]$](img4.gif) or explain why it can't be created with
this type.
or explain why it can't be created with
this type.
- (5 points) Can this filter be type II? Either give an
example impulse response
![$h[n]$](img4.gif) or explain why it can't be created
with this type.
or explain why it can't be created
with this type.
- (5 points) Can this filter be type III? Either give an
example impulse response
![$h[n]$](img4.gif) or explain why it can't be created
with this type.
or explain why it can't be created
with this type.
- (5 points) Can this filter be type IV? Either give an
example impulse response
![$h[n]$](img4.gif) or explain why it can't be created
with this type.
or explain why it can't be created
with this type.
- (25 points) Short Answer
- (5 points) Can an all-pass filter be minimum phase? Either
give an example or explain why it is not possible.
- (5 points) Is it possible for a minimum phase FIR filter to
have linear phase? Either give an example or explain why it is
not possible.
- (5 points) You are given a stable pole-zero system with all
of its poles inside the unit circle. Does this system have to be
causal? Either explain why the system has to be causal or provide
a counter example.
- (5 points) Given a pole/zero plot with poles at .9j and -.9j
and zeros at .9 and -.9, sketch the magnitude of
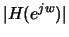 .
.
- (5 points) Given the following filter:
Derive 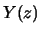 as a function of
as a function of 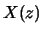 .
.



Next: EEL6586: HW#2
Up: EEL6586: Homework
Previous: EEL6586: Homework
Dr John Harris
2006-04-17
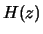 and sketch
them on a pole/zero plot. State the ROC.
and sketch
them on a pole/zero plot. State the ROC.
![$h[n]$](img4.gif) from the given
from the given 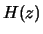
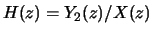
![$h[n]$](img4.gif) .
.
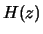 . (Note: you can do this part even if you are not able to
complete part b).
. (Note: you can do this part even if you are not able to
complete part b).
![$h[n]$](img4.gif) or explain why it can't be created with
this type.
or explain why it can't be created with
this type.
![$h[n]$](img4.gif) or explain why it can't be created
with this type.
or explain why it can't be created
with this type.
![$h[n]$](img4.gif) or explain why it can't be created
with this type.
or explain why it can't be created
with this type.
![$h[n]$](img4.gif) or explain why it can't be created
with this type.
or explain why it can't be created
with this type.
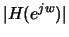 .
.
![\begin{displaymath}
y[n] = \sum_{k=-\infty}^n x[k]
\end{displaymath}](img9.gif)