


Next: EEL6586: HW#3
Up: EEL6586: Homework Assignments
Previous: EEL6586: HW#1
Get PDF file
Due Friday, Feb 15, 2002 in class. Late homework will lose
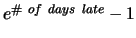 percentage points. To see the current
late penalty, click on
percentage points. To see the current
late penalty, click on
http://www.cnel.ufl.edu/hybrid/harris/latepoints.html
PART A: Noncomputer Problems
- A1
- Suppose you are estimating a short-term average magnitude function
using a 200 point Hamming window for a 10KHz sampled speech waveform.
Using Nyquist arguments and some simple assumptions, what is the most you
can reasonably shift the window between applications without losing
information?
- A2
- The short-term energy of a sequence
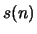 is defined as
is defined as
- i
- For the particular choice
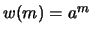 for
for 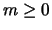 and 0 otherwise,
find a recurrence formula for
and 0 otherwise,
find a recurrence formula for 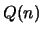 in terms of
in terms of 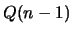 and the input
and the input
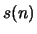 .
.
- ii
- What general property must the window
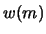 have in order that it
be possible to find a recursive implementation?
have in order that it
be possible to find a recursive implementation?
- A3
- Consider the signal
- i
- Find the long-term autocorrelation function
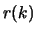 for
for 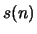 .
.
- ii
- Sketch (by hand)
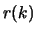 as a function of
as a function of 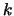 . Label important points.
. Label important points.
- A4
- A train of impulses is fed through an all-pole model of
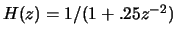 . Sketch the time domain waveform for a few
periods assuming
. Sketch the time domain waveform for a few
periods assuming 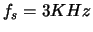 and pitch frequency is 300 Hz. Label all
important parameters. Show all of your hand calculations, you may
check your results with Matlab if you want.
and pitch frequency is 300 Hz. Label all
important parameters. Show all of your hand calculations, you may
check your results with Matlab if you want.
- A5
- Sketch the magnitude of the Fourier Transform for the all-pole
signal created in problem A4. Label all important parameters.
PART B: LPC Example
Consider the infinite-length signal
Your goal is to derive the LPC
coefficients for the prediction of 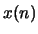 . Assume order
. Assume order 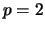 (that is, you will only consider the two previous
values in predicting the next one).
(that is, you will only consider the two previous
values in predicting the next one).
- B1
- Compute the autocorrelation matrix R (Assume an extremely long
window and include a
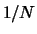 normalization factor for parts B1 and
B2).
normalization factor for parts B1 and
B2).
- B2
- Compute cross correlation vector
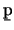 .
.
- B3
- Compute the two LPC coefficients for this problem.
- B4
- What is the resulting error in prediction?
- B5
- Sketch the magnitude response of the all-pole estimator for this
signal (
 ).
).
PART C: Computer Analysis of Speech
You will write a program to segment a recorded sentence into three
different components: silence (non-speech), voiced speech and
unvoiced speech. You should run your code on the sentence found
at
http://www.cnel.ufl.edu/analog/courses/EEL6586/sentence.html.
- C1
- Describe (in words) your strategy in writing and improving your
program. A successful labeling program should utilize at least a
short-term energy and a short-term zero crossing measure. However, as
usual, you may add whatever you like to further improve the performance of
your program. Make sure to turn in all code you use as the appendix of this homework.
- C2
- Show a plot that, you feel, best depicts the labeling of the test sentence.
- C3
- Have matlab create a table of the starting location of each labelled segment. For instance, your output should look something like the following:
| Sample Number |
Type |
| 1 |
silence |
| 234 |
unvoiced |
| 578 |
voiced |
- C4
- Comment on the accuracy of your algorithm. Make sure to run your code on other sentences to see how generally is can be
applied. Show the labeling for one other sentence that you have recorded. In what cases does your algorithm tend to
have problems?
- C5
- Using your algorithm, estimate the ratio of the average power in voiced vs.
the average power in unvoiced phonemes in normal speech (in dB). You can do this by looking at the average energy
per frame. Also estimate the rough percentages of energy
in voiced and unvoiced phonemes in normal speech (now you must consider duration and frequency of occurence).



Next: EEL6586: HW#3
Up: EEL6586: Homework Assignments
Previous: EEL6586: HW#1
Dr John Harris
2002-04-27
![\begin{displaymath}Q(n)=\sum_{m=-\infty}^\infty [s(m)w(n-m)]^2 \end{displaymath}](img6.gif)
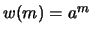 for
for 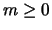 and 0 otherwise,
find a recurrence formula for
and 0 otherwise,
find a recurrence formula for 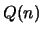 in terms of
in terms of 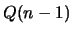 and the input
and the input
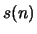 .
.
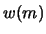 have in order that it
be possible to find a recursive implementation?
have in order that it
be possible to find a recursive implementation?
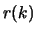 for
for 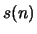 .
.
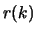 as a function of
as a function of 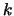 . Label important points.
. Label important points.