EEL6502: Exam#1

1. (25 points)

   Consider the infinite-length signal x(n), a short segment is shown above. Your goal is to derive the causal Wiener filter for the single step prediction of x(n). Assume two taps (L=2).

   1. (5 points) Compute the autocorrelation matrix R.

   2. (5 points) Compute the cross correlation vector .

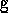   3. (5 points) Compute the optimal filter .

   4. (5 points) Compute 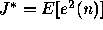for the Wiener filter.

   5. (5 points) Considering your answer to (c) and (d) above, explain in words the algorithm the system uses to predict the next value.

2. (25 points)

   Consider the problem of solving a system ID problem where the input signal is and the ``unknown'' filter is an FIR filter with h(0)=1 and h(1)=1.

   1. (5 points) Compute the autocorrelation matrix R. Big Hint: you can use the result given in problem 3.14 in Clarkson.

   2. (5 points) Compute the cross correlation vector .

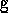   3. (5 points) Compute the optimal causal filter .

   4. (5 points) Describe what happens when 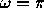. What is ?

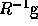   5. (5 points) Describe the optimal filter for .

3. (25 points)

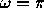   Consider the above equalization problem. The channel h(n) is simply a scaling function, that is where k is an arbitrary scaling constant. The variance of the zero-mean, white noise is .

   1. (5 points) How many taps are necessary for the optimal filter (f(n)) to produce zero error? (L=?)

   2. (5 points) Write J as an explicit function of f(0) Use 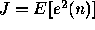and assume L=1 for the rest of this question.

   3. (5 points) Derive .

   4. (5 points) Derive the iterative gradient descent formula for 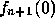. Remember the gradient descent equation we used in class was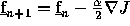

   5. (5 points) What value of the step size ( 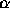) leads to the fastest possible convergence?

4. (25 points) Short Answer.
   1. (5 points) Compute E[e(n)y(n)] for the Wiener filter.

   2. (5 points) You are given a signal 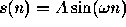where A is a random value selected from a uniform distribution between -1 and +1 for each ensemble. Is this signal stationary? Think carefully about this, draw a few representative examples and remember that in class we defined stationary to mean that the statistical properties we typically measure are independent of the value of n.)

   3. (5 points)

      Consider the above system ID problem where the unknown filter h(n) is an FIR filter with M taps and the optimal filter f(n) is an FIR filter with L taps. Assume that L<M. w(n) is zero mean, white Gaussian noise with variance 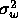. Is the following condition guaranteed to hold. Explain why or why not.

      

   4. (5 points)

      Are all stable AR sequences stationary? Explain why or why not.

   5. (5 points)

      What is the optimal two-sided, -length solution for F(z) in the above prediction problem?