EEL6502: Exam1

1. (25 points) You goal is to use an adaptive filter to design a single-step linear predictor for the following signal:

   

   where is zero-mean Gaussian noise with a variance of one.

   1. (5 points) Draw an adaptive filter block diagram for a single-step linear predictor architecture.

   2. (10 points) Assume that you only use two taps in your adaptive filter, compute the value of the weights for the optimal Wiener filter. (Of course your filter is causal)

   3. (5 points) Compute the MSE for the Wiener filter.

   4. (5 points) Suppose that we would like to predict the signal two steps into the future. How many taps do you need to have for minimum prediction error? Explain.

2. (25 points) 

   

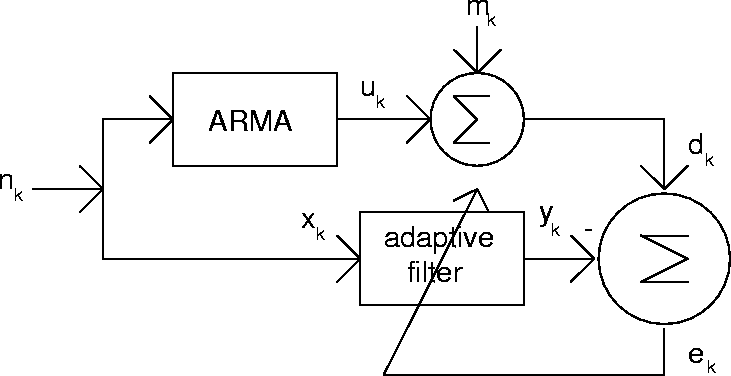
   This problem relates to the system ID problem shown above. Assume that is generated by a first order ARMA process with fixed values a and b such that:

   

   Assume and are zero-mean gaussian noise processers with a variances of and respectively. You may assume that |a|<1 and |b|<1.

   1. (5 points) Compute the z-transform of the tap weights for the infinite, two-sided Wiener solution for this problem.

   2. (5 points) Compute the individual weight values for the stable, infinite, two-sided Wiener solution. (Be sure to specify all of the values).

   3. (5 points) Compute the MSE for the infinite two-sided Wiener solution.

   4. (5 points) Now we would like to compute the Wiener solution for a causal finite-filter length. Identify the weight values if we consider a casual filter with L+1 taps.

   5. (5 points) Compute the MSE for the finite, casual filter in Part d above.

3. (25 points) Consider the adaptive noise cancellation problem where the primary signal is zero-mean Gaussian noise with variance ( ) and the reference signal is equal to one ( ). Answer the following questions about the LMS implementation of this adaptive filter using a step size parameter . Remember that you only need one tap weight for this problem.
   1. (5 points) Using the approximations derived in class (and also in the book), estimate the variance of the the weight value after ``convergence.''
   2. (10 points) Compute an exact expression for the variance of the weight.
   3. (10 points) Compute an exact expression for the Misadjustment M.

4. (25 points) Answer each of the following short answer problems. Explain your answers.
   1. (5 points) Describe how the performance surface changes if each value of the the desired signal 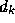exactly doubles in value and the values of 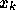remains at their original level. Your answer should discuss the exact nature of the changes in steepness of the bowl of the performance surface as well as the height ( 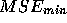) and location of the minimum ( ).
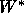   2. (5 points)

      

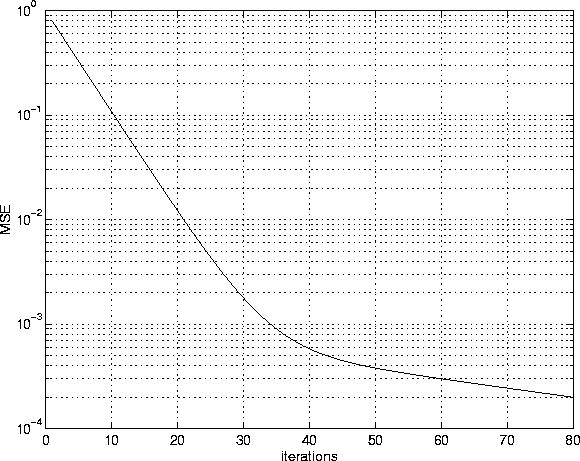
      The above plot shows the convergence of the MSE for a steepest descent algorithm. Use the plot to estimate the eigenvalues of the R matrix. Assume that , , 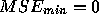and that there are only two taps.

   3. (5 points) Our goal is to develop a classical LMS-based Adaptive Noise Cancellation system similar to the one you wrote for HW4. The only additional constraint is that there will be long periods of time when the noise interference completely disappears, i.e. the reference signal becomes exactly zero. (We are assuming no leakage of the signal into the reference). Describe the simplest modification of the architecture that will prevent the weights from changing to erroneous values during these deadtimes.
   4. (5 points) For an optimal Wiener filter, is it possible for an increase in the number of taps to result in a higher MSE? Explain. Show an example if necessary.
   5. (5 points) We would like to change the frequency of a sine wave using an LMS adaptive filter of the type we have discussed in class. For simplicity we choose a desired signal (d) to be a 1KHz sine wave and an input signal (x) as a 2KHz sine wave. We would like the output y to be at a frequency of 1KHz. Describe the important issues involved in the successful implementation of such an adaptive filter (e.g. necessary number of taps, value of 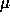, value of error, etc.).