EEL5701: MATLAB#5

Due Tuesday, August 5 at the beginning of class Please turn in all of the Matlab code that you write. This is your last Matlab assignment of the semester.

Your goal is to design a discrete-time Butterworth IIR filter that meets the following specifications:

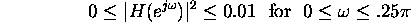
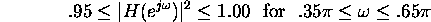
Note that this specification is slightly different from that used in M#4.

The following questions will lead you through the complete design by first constructing a continuous-time low-pass filter, mapping to discrete-time using the bilinear transform, and finally mapping to a bandpass filter using the appropriate discrete to discrete mapping given in Table 7-1 in O&S. You will do all of this without using the butter command given in Matlab.

Clearly answer the following questions and explain your work.

1. Derive specifications for the allowed ripple in the pass and stop bands. (e.g., 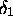and ).
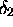2. Derive the 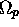and 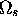for the analog filter. Remember to consider the warping due to the bilinear transformation.
3. Compute the minimum order (N) Butterworth filter that can meet the specifications. N must be an integer, check your result with the buttord function in Matlab (make sure you call the function with the proper arguments).
4. Write down the Laplace transform of the continuous-time filter ( 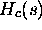). You may use Matlab to help you generate the poles.
5. Derive the H(z) that results from the bilinear transformation. You may use the bilinear command in Matlab.
6. Map the low-pass H(z) to the correct bandpass filter using the appropriate transformation given in Table 7-1 in O&S. What is the new H(z)?
7. Plot the magnitude of the frequency response and show that the filter meets the original specifications. (Use log or linear scales, whichever you fell best shows the specifications are satisfied).

8. Plot the pole/zero diagram for the filter. Intuitively explain why their locations make sense for the filter you designed.
9. Plot the impulse response (e.g. use the filter command). What is the delay of this filter?
10. Generate another butterworth filter using the butter command in MATLAB. Use something like the following:

    [N, Wn] = buttord(Wp, Ws, Rp, Rs) 
    [b,a] = butter(N,Wn)

    Compare the magnitude of the frequency response compared to the filter you already designed. Explain any differences.
11. Finally, filter the signal given in http://www.cnel.ufl.edu/analog/courses/EEL5701/m5.asc The file consists of 30,000 ascii numbers between +1 and -1. A zip file (m5.zip) also exists. Plot a sample of the signal before and after filtering. Plot the magnitude of the FFT of the signal before and after filtering. (A log plot may be more informative than a linear one).
12. The signal is digitized sound that can be heard using the sound command in MATLAB. The sampling rate is 5512Hz. Listen to the signal before and after filtering using the Matlab sound command. Describe what you hear.